Реферат: Гамма функции

и на основании (2.2) имеем

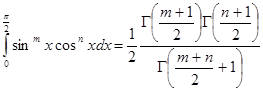(3.1)

В интеграле

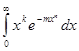
Где k > -1,n > 0,достаточно положить

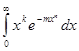
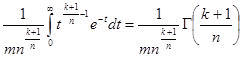
17

Интеграл

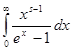
Где s > 0,разложить в ряд

=

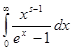
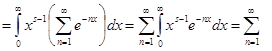
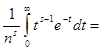
где дзетта функция Римана

Рассмотрим неполные гамма функции (функции Прима)

связанные неравенством

Разлагая, в ряд имеем

18

Переходя к выводу формулы Стирлинга , дающей в частности приближенное значение n! при больших значениях n ,рассмотрим предварительно вспомогательную функцию

(3.2)

Непрерывна на интервале (-1,) монотонно возрастает от до при изменении от до и обращаются в 0 при u = 0.Так как

то при u > 0 и при u < 0 , далее имеем

И так производная непрерывна и положительна во всем интервале ,удовлетворяет условию

19

Из предыдущего следует, что существует обратная функция, определенная на интервале непрерывная и монотонно возрастающая в этом интервале,

Обращающаяся в 0 при v=0 и удовлетворяющая условие

(3.3)

Формулу Стирлинга выведем из равенства

полагая ,имеем

Положим далее введенная выше обратная функция, удовлетворяющая условиям u = -1при ,и при .Замечая что(см.3.2)

20

имеем

,

полагая на конец ,,получим

или

в пределе при т.е. при (см3.3)

откуда вытекает формула Стирлинга

которую можно взять в виде

21

(3.4)

где ,при

для достаточно больших полагают

(3.5)