Реферат: Геодезические работы при составлении топоплана
При измерении наклонных расстояний горизонтальное проложение определяют:
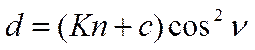
v - угол наклона визирной оси зрительной трубы.
IV.Геодезические сети
Вопрос: В чем сущность прямой и обратной геодезической задач?
Прямая геодезическая задача
Для решения геодезических задач в строительстве наиболее целесообразной является система прямоугольных координат в проекции Гаусса—Крюгера. Для определения координат последующих точек при известных координатах начальной точки, известных расстояниях между точками и известных дирекционных углах сторон между точками решается прямая геодезическая задача.
Пусть имеем точку А с координатами XA и YA , а координаты точки В' обозначим через Х'B и Y'B (рис3). Проведем через точку A линию, параллельную оси абсцисс, а через точку В' — линию, параллельную оси ординат. В результате получим прямоугольный треугольник, катеты которого будут равны разностям координат:
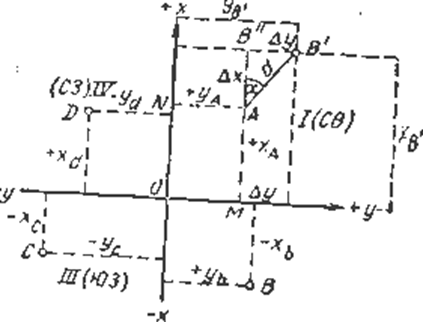
AВ" = XB . - XA .
В'B"=YB '-YA '
или
ХВ '– YА = ± Δх
YВ' – YА = ± Δ y
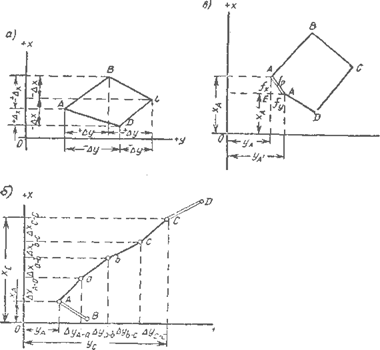
Рис 4
Величины Δх и Δy называются приращениями координат.
Зная значения Δ х и Δy стороны АВ' и координаты
начальной точки А, можно определить координаты конечной точки В'
XB '=XA _±ΔX
YB '=YA ± Δy
Иначе говоря, координата точки последующей равна координате точки предыдущей плюс соответствующее приращение, т. е. в общем случае:
Xn=Xn-1 +ΔX
Yn=Yn-1 +ΔY
В зависимости от направления стороны АВ' приращения координат Δх и Δ у могут иметь знак плюс или знак минус. Знаки приращений координат определяют по направлениям сторон, т. е по их дирекционным углам.
Из рис. видно, что: Δх=dcosαΔy = dsinα
Из рассмотрения (рис.4) следует, что приращения Δх и Δу координат есть не что иное, как ортогональные проекции горизонтального расстояния d между точками A и B' и другими на оси координат. Формулы являются формулами решения прямой геодезической задачи. Знаки приращений координат совпадают со знаками тригонометрических функций (соответственно синуса и косинуса дирекционного угла).
Приращения координат могут быть вычислены тремя способами: по таблицам натуральных значений тригонометрических функций; по таблицам логарифмов и по специальным таблицам для вычисления приращений координат, правила пользования, которыми изложены в объяснении к таблицам.
В практике геодезических работ для строительства приходится определять координаты не какой-либо одной точки, а ряда точек, связанных между собой горизонтальными приложениями между точками и дирекционными углами сторон, заключенных между этими точками.
Обратная геодезическая задача
В практике строительства весьма часто приходится определять длину стороны и ее дирекционный угол по известным координатам ее конечных точек, т. е. решать обратную геодезическую задачу. Такая задача возникает при проектировании и перенесении объектов строительства на местность.
Если известны координаты двух точек B' и А (см. рис4.), т. е. известны приращения координат по стороне АВ', то тангенс дирекционного угла стороны АВ' определяется из треугольника АВ"В':
tgα=Δy/Δx
Из формулы можно написать:
d=Δx/cosα d=Δy/sinα
D=√ (Xb'-Xa)2 +(Yb'-Ya)2 =√Δx2 +Δy2
При решении обратных геодезических задач пользуются пятизначными таблицами логарифмов. Для определения величины дирекционного угла четверть устанавливают по знакам приращений координат.
При наличии малых вычислительных машин и значительном количестве задач решение их рациональнее выполнять нелогарифмическим способом, пользуясь пятизначными таблицами натуральных значений тригонометрических функций.
Задание2 Решение задач
Задача 1 Определить дирекционные углы линий ВС и СД, если:
![]() ;
;
![]()
![]()
![]()
![]()
![]() =236гр 40,2мин.-189гр59,2мин=46гр41мин
=236гр 40,2мин.-189гр59,2мин=46гр41мин