Реферат: Геометричні фігури на площині та їх площі

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

ЛУБЕНСЬКА ЗАГАЛЬНООСВІТНЯ ШКОЛА № 3

І-ІІІ СТУПЕНІВ

РЕФЕРАТ

НА ТЕМУ:

ГЕОМЕТРИЧНІ ФІГУРИ НА ПЛОЩИНІ ТА ЇХ ПЛОЩІ

Виконала: учениця 5-Б класу

Німець Євгенія

Лубни 2007

Вступ

Даний реферат охоплює геометричні фігури, що розглядаються в планіметрії - розділі геометрії, в якому вивчають фігури на площині, тобто, так би мовити, у двовимірному світі.

Основними геометричними фігурами на площині є точка і пряма . Я дам їх визначення, як також визначення кута , трикутника , квадрата , чотирикутника , ромба , паралелограма , трапеції , многокутника . Пригадаю, як визначали площі згаданих фігур у часи античності та сучасні методи обчислення площ.

Точка і пряма

Як вже було зазначено, точка і пряма є основними геометричними фігурами на площині. Математично, точкою на площині є об’єкт, два плоскі виміри якого (x і y ) прямують до нуля. Тобто, це об’єкт, що має плоскі координати x і y , але не має розмірів, тобто довжини і ширини, тобто це „існуюче ніщо”. Як би я не загострювала кінчик олівця, в надії нанести на площину математичну точку - в мене нічого не вийде. Реально нарисована точка матиме цілком реальні (хай навіть менше 0,1 мм!) розміри по x та по y . Таке визначення точки у математиці було зроблено для спрощення розрахунків.

Як правило, всяку геометричну фігуру прийнято вважати складеною з точок. Тому прямою на площині (рис.1) є геометричне місце точок, один з вимірів якого (скажімо довжина) рівний нескінченності, а інший - ширина, прямує до нуля. Для порівняння, відрізок ( рис 2), як частина прямої , яка складена з усіх точок прямої, що лежать між двома її точками, має нульову ширину при цілком певній довжині , скажімо 15 см чи 5 м. Півпрямою , або променем ( рис.3) називають частину прямої, яка складається з усіх точок цієї прямої, що лежать по один бік від даної на ній точки. Промінь також вважають проведеним у нескінченність в один бік.

Аналогічно попередньому, яким тонким не був би кінчик мого олівця, я не зможу накреслити математичну пряму, відрізок чи промінь - вони матимуть цілком певну ширину.

а

рис.1

А В

Рис. 2.

???.3

Кут

Кутом ( ???.4) ??????????? ??????, ?? ??????????? ? ???? ?????? ????????? ?? ???????? ?????????? ??????, ??? ??????????? вершиною ????, ? ???????? - сторонами ????.

Рис.4

Очевидно, що до фігур, зазначених вище, поняття площі незастосовне .

Плоскі геометричні фігури

Чотирикутником взагалі є фігура, складена з чотирьох точок і чотирьох відрізків, які послідовно їх сполучають. Чотирикутник називають опуклим , якщо він розміщений в одній півплощині відносно прямої, яка містить будь-яку його сторону. На рисунках 5 і 6 показано опуклий та неопуклий чотирикутники.

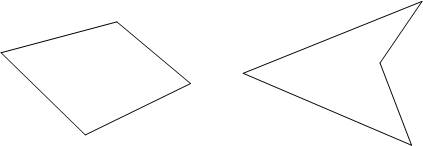Рис.5 Рис.6

Сторони чотирикутника, що виходять з однієї вершини, називають сусідніми сторонами, а сторони, які не мають спільного кінця - протилежними сторонами.

Прямокутник (рис.7) - це чотирикутник, у якого всі кути прямі.

b

а

Рис. 7.

Як бачимо з рис.7, геометри античності спочатку розбивали прямокутник на квадратики, які були одиницями площі (поняття метр і метр квадратний з’явилось пізніше) і підраховували їх кількість. Тепер використовується формула S _прям. = аb .

Квадрат - це прямокутник, у якого всі сторони рівні (рис.8).

а

Рис.8

Можна також розбити квадрат на n одиниць площі і знайти їх суму, проте ми користуємося формулою S _квад. = а ² .

--> ЧИТАТЬ ПОЛНОСТЬЮ <--