Реферат: Главные движущие силы землетрясений, дрейфа континентов и горообразования. Прогнозирование землетрясений и спусковые силы
Мы можем оценить некоторые параметры мантийных конвекционных потоков. Вертикальные столбы мантийного вещества под приведенными поверхностями в зоне восходящего и нисходящего потоков от поверхности до низа слоя конвекции имеют приблизительно равные веса (и массы). Поэтому по толщине слоя конвекции H и по разности высот приведенного уровня ![]() H можно вычислить разность температур
H можно вычислить разность температур ![]() T в восходящей и нисходящей частях потока, задавшись значением коэффициента температурного расширения:
T в восходящей и нисходящей частях потока, задавшись значением коэффициента температурного расширения: ![]() T =
T = ![]() H / (H*k) = 7500м / (2 800 000м * 0.00001/1°С)
H / (H*k) = 7500м / (2 800 000м * 0.00001/1°С) ![]() 270°С. Здесь H = 2 800 000 м - толщина конвекционного слоя, k = 0.00001/1°С - линейный коэффициент температурного расширения.
270°С. Здесь H = 2 800 000 м - толщина конвекционного слоя, k = 0.00001/1°С - линейный коэффициент температурного расширения.
Исходя из теплоемкости мантийного вещества (для базальта Сq ![]() 660 ккал/( кубич.метр * градус С)), величины теплового потока (Q = 800-8000 ккал/(год*м2)) и только что вычисленной разности температур (270°С) в восходящей и нисходящей частях потока, можно вычислить скорость V мантийного конвекционного потока, доставляющего тепло из глубин к коре (которое и наблюдается как поток глубинного тепла через поверхность коры).
660 ккал/( кубич.метр * градус С)), величины теплового потока (Q = 800-8000 ккал/(год*м2)) и только что вычисленной разности температур (270°С) в восходящей и нисходящей частях потока, можно вычислить скорость V мантийного конвекционного потока, доставляющего тепло из глубин к коре (которое и наблюдается как поток глубинного тепла через поверхность коры).
Q = (Сq * Т) * V ; V = Q / ( Т * Сq) = 800-8000 (ккал/(год*м2))/(270*660) = 5-50 мм/год.
Приняв, что горизонтальное сечение конвекционного потока на 1/3 восходящее, на 1/3 нисходящее, на 1/3 неподвижное, получим скорость потока от 15 мм/год до 150 мм/год, что приблизительно совпадает со скоростью смещения литосферных плит в ходе спрединга. Для более точного определения скорости конвекционного мантийного потока нужно уточнить исходные параметры и геометрическую конфигурацию этого потока.
Отметим, что с целью более наглядного раскрытия механизма работы мантийных конвекционных потоков и вязкого увлечения ими литосферных плит (приводящего к их дрейфу) мы оставляем за рамками рассмотрения взаимно компенсирующееся адиабатическое понижение-повышение температуры при понижении-повышении давления в восходящих - нисходящих частях этих потоков и другие детали процессов, фиксируясь на главном. Подчеркнем, что движение литосферных плит обусловлено именно тем, что мантийные потоки увлекают, тянут их. Ведь если бы плиты соскальзывали по наклонной приведенной поверхности опережающими темпами (по сравнению с потоком), то они достаточно быстро заполнили бы и совсем ликвидировали впадину на этой приведенной поверхности.
Силу вязкого трения, действующую со стороны движущейся вязкой магмы на участок твердой коры шириной ![]() W = 1м, расположенный на наклонной и нижней частях поверхности приведенного уровня (усилие передается и по твердой коре от более высоко расположенных участков ко всем нижележащим), можно легко подсчитать, опираясь только на геометрию приведенной поверхности. А не на неизвестное пока значение вязкости мантийного вещества. Это возможно, поскольку в форме приведенной поверхности и проявляются вязкие свойства движущегося мантийного вещества. Причем может оказаться, что величина вязкости подкоровой магмы на разных глубинах и в различных частях конвекционного потока различна (вязкость зависит от температуры и давления, т.е., глубины расположения поверхности раздела М). О вязкости магмы под корой можно будет судить по форме поверхности приведенного уровня. Эти уточнения можно будет сделать после более точного определения формы поверхности приведенного уровня:
W = 1м, расположенный на наклонной и нижней частях поверхности приведенного уровня (усилие передается и по твердой коре от более высоко расположенных участков ко всем нижележащим), можно легко подсчитать, опираясь только на геометрию приведенной поверхности. А не на неизвестное пока значение вязкости мантийного вещества. Это возможно, поскольку в форме приведенной поверхности и проявляются вязкие свойства движущегося мантийного вещества. Причем может оказаться, что величина вязкости подкоровой магмы на разных глубинах и в различных частях конвекционного потока различна (вязкость зависит от температуры и давления, т.е., глубины расположения поверхности раздела М). О вязкости магмы под корой можно будет судить по форме поверхности приведенного уровня. Эти уточнения можно будет сделать после более точного определения формы поверхности приведенного уровня:
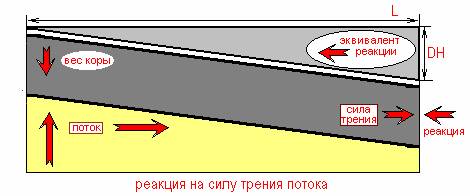
Рассмотрим рисунок, на котором изображен профиль наклонной части приведенной поверхности мантийного конвекционного потока. Здесь воздействие воображаемого тяжелого верхнего треугольника (с плотностью мантии d) компенсирует вертикальную и горизонтальную составляющие силы, действующей на кору со стороны нижележащей магмы. На самом же деле, горизонтальная составляющая (с которой кора увлекается движущейся магмой) компенсируется не действием воображаемого треугольника, а реакцией жесткой коры справа. Просто эта реакция коры эквивалентна воздействию воображаемого треугольника, а его легко подсчитать. В результате увлечения коры вязким потоком в большей части жесткой коры (почти повсеместно, за исключением вершины купола и других особенных точек, скажем в окрестностях разрыва или щели в коре) возникает напряжение сжатия, которое можно легко подсчитать.
F = ![]() g * d *
g * d * ![]() W * (
W * (![]() H)2
H)2
Правильность этого выражения подтверждается уже тем, что точно такое же выражение мы имеем для силы, действующей на боковую стенку прямоугольного сосуда, наполненного жидкостью до высоты H.
![]()
В соответствии с полученным выражением для горизонтального сжатия в зоне нисходящего потока (под Гималаями, считая линию сжатия параллельной линии спрединга) имеем: F = ![]() *9.8 (м/сек2) * 3300(кг/м3) * 1м * (7 500 м)2 = 91 * 1010 н.
*9.8 (м/сек2) * 3300(кг/м3) * 1м * (7 500 м)2 = 91 * 1010 н.
Эта горизонтальная сила приложена перпендикулярно к вертикальной полосе, секущей твердую кору сверху донизу. Тогда на каждый 1м2 сечения коры (толщиной 90 км) в среднем приходится сила 1*107 н (=100кгС/см2). Это примерно 1/20 предела прочности монолитного гранита в наилучших условиях (200 МПА для одноосевого сжатия при обычной температуре). Но это в среднем. На практике же, и прочность пород из-за дефектов меньше даже при низкой температуре (в верхних слоях коры), и эффективная толщина коры меньше, и перепад высот приведенных уровней может быть больше. Кроме того, большая часть сечения коры имеет высокую температуру, отчего ее прочность существенно уменьшается. Так что эффективные напряжения одноосевого (в направлении от восходящего потока к нисходящему) сжатия в твердой коре над нисходящими частями вязкого конвекционного потока вполне достаточны для превышения предела прочности пород, составляющих кору, и выдавливания в этих зонах из коры гор (в моменты землетрясений).
Если напряжения сжатия недостаточны для преодоления предела прочности, то пластические деформации не происходят, просто кора несколько напряжена - упруго деформирована. Если же сжатие так велико, что превышается предел прочности, то в результате очередного землетрясения с очагом в некоторой точке (быстрой пластической деформации) вдоль линии сжатия, проходящей через очаг землетрясения, напряжение сжатия разряжается. Тогда как в прилегающих областях (вокруг этой линии) напряжение сжатия скачком возрастает (из-за некоторого смещения коры как целого), в результате чего может иметь место такое явление, как форшоки и афтершоки. Аналогичная картина наблюдается не только при сжатии соседних плит коры, но и при их относительном сдвиге.
Средний темп генерации гор на всей Земле за счет их выдавливания из зоны сжатия составляет: ![]() V = длина растущих гор (=60000км) * выдавливаемая часть толщины коры (=1/6Н=5км) * скорость сближения плит (=2см/год)
V = длина растущих гор (=60000км) * выдавливаемая часть толщины коры (=1/6Н=5км) * скорость сближения плит (=2см/год) ![]() V
V ![]() 6 кубических километров в год на всей Земле.
6 кубических километров в год на всей Земле.
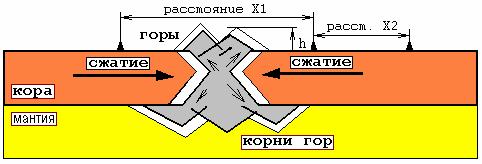 Выдавливание гор на границе плит.
Выдавливание гор на границе плит.
Причем поперечное сечение выдавливаемого горного хребта (S=![]() *B*h) увеличивается, в среднем, с постоянной скоростью (для Гималаев S = (1/6Н=15км) * (=2см/год)
*B*h) увеличивается, в среднем, с постоянной скоростью (для Гималаев S = (1/6Н=15км) * (=2см/год) ![]() 300 м2 в год). Отсюда следует вывод, что высота гор h (при прочих равных условиях) меняется гораздо быстрее у низких гор (когда ширина основания горного хребта B мала). Если для Гималаев мы примем ширину зоны горного хребта, испытывающего поднятие в настоящее время, равной 60 км, то получим скорость роста высоты гор в этой поднимающейся зоне порядка 1 см/год, или 1 метр за 100 лет (без учета их разрушения). Отметим также, что, имея данные о скорости сближения плит, о скорости увеличения высоты гор, зная толщину коры и сечение горного хребта, легко увидеть, какая часть толщины коры выдавливается в виде гор вверх (действительно ли 1/6?), а какая - в виде корней гор вниз в ходе сближения плит.
300 м2 в год). Отсюда следует вывод, что высота гор h (при прочих равных условиях) меняется гораздо быстрее у низких гор (когда ширина основания горного хребта B мала). Если для Гималаев мы примем ширину зоны горного хребта, испытывающего поднятие в настоящее время, равной 60 км, то получим скорость роста высоты гор в этой поднимающейся зоне порядка 1 см/год, или 1 метр за 100 лет (без учета их разрушения). Отметим также, что, имея данные о скорости сближения плит, о скорости увеличения высоты гор, зная толщину коры и сечение горного хребта, легко увидеть, какая часть толщины коры выдавливается в виде гор вверх (действительно ли 1/6?), а какая - в виде корней гор вниз в ходе сближения плит.
Высота гор растет до предела, обусловленного прочностью пород (R 200 МПА для одноосевого сжатия гранита и базальта без дефектов) и силой тяжести g на планете. При превышении этого предела начинает выдавливаться новый горный хребет, почти параллельный предыдущему - генерируется целая горная провинция. По этой причине высота гор на Земле (h) ни при каких условиях не может быть больше 14.8 км ![]() 2 * 7.4 км (200 МПА >
2 * 7.4 км (200 МПА > ![]() (g * d * h) =
(g * d * h) = ![]() (9.8*2800*7400)). Коэффициент 2 появляется из-за того, что горы не параллелепипеды, а, скорее, лежащие на боковой грани треугольные призмы с сечением S=
(9.8*2800*7400)). Коэффициент 2 появляется из-за того, что горы не параллелепипеды, а, скорее, лежащие на боковой грани треугольные призмы с сечением S=![]() *B*h. Поскольку реально высота гор от подножия до вершины (а не над уровнем моря) не превышают 5 км, мы должны сделать вывод, что эффективная прочность пород коры, по крайней мере, втрое меньше взятой из справочника (для бездефектного образца).
*B*h. Поскольку реально высота гор от подножия до вершины (а не над уровнем моря) не превышают 5 км, мы должны сделать вывод, что эффективная прочность пород коры, по крайней мере, втрое меньше взятой из справочника (для бездефектного образца).
То есть, из-за различных дефектов в теле гор, а также из-за дополнительного сопротивления (сверх преодолеваемого литостатического давления выдавливаемых гор) при их выдавливании из коры, горы на Земле никогда не достигают максимально возможной высоты (соответствующей прочности бездефектных пород). Даже под водой, где часть давления горы компенсируется давлением воды. Кстати, по этой причине подводные горы могут иметь несколько большую крутизну и высоту, чем горы на суше. Еще большую высоту могут иметь горы на небесных телах с меньшей, чем на Земле, силой тяжести. Так, конусообразная (а не призматическая!) гора Олимп на Марсе имеет высоту порядка 24 км.
Отметим, что при выдавливании из материковой коры гор площадь самой материковой плиты (того образования, которое мы сегодня видим как материковую плиту) со временем слегка уменьшается. Это замечание позволяет точнее увидеть баланс площадей материков и океанов в относительно близком геологическом прошлом.
В далеком же прошлом потоки глубинного тепла были в K раз больше нынешних, конвекционные потоки были интенсивнее, а кора была в K раз тоньше [2]. Поскольку непосредственно под тонкой корой и давление было меньше, и температура выше, магма непосредственно под корой в то время была менее вязкой. Менее вязкая магма увлекала кору с меньшей силой. Поэтому в зонах нисходящих мантийных потоков в те времена не развивались такие огромные усилия, как в настоящее время, т.е. вязкое увлечение коры магмой в те времена было недостаточно сильным для интенсивного горообразования в этих зонах (для пластической деформации коры). Кора над нисходящими потоками при относительно малом давлении под ней и тогда была достаточно толстой, чтобы выдержать относительно слабое сжатие. Над нисходящими потоками температура уже слегка остывшего мантийного потока была минимальной, поэтому наиболее тугоплавкие вещества из состава мантии кристаллизовались здесь на нижней поверхности коры более интенсивно, чем в зоне восходящего потока. Равновесие наступало из-за уменьшения скорости отвода тепла (в том числе, тепла кристаллизации) через более толстую кору. Скажем, для теплового потока, большего, чем сегодняшний, в 10 раз, толщина коры составляла 5 км. В итоге приходим к выводу, что во времена более интенсивных потоков тепла из глубин планеты интенсивность тектонических процессов была намного ниже нынешней из-за гораздо меньшей вязкости магмы непосредственно под тонкой корой.
Прямую аналогию, подтверждающую наши выводы, мы видим в Северном ледовитом океане. Площадь здешних льдов сравнима с площадями литосферных плит, скорости течений, увлекающих льды, намного больше скоростей древних мантийных потоков. Вязкость воды лишь немного меньше вязкости жидкой магмы под тонкой древней корой (и высокотемпературной магмы из нынешних вулканов), и на много порядков меньше вязкости нынешней мантии. Поэтому и не наблюдаем мы в Северном ледовитом океане многокилометровые ледяные горы, но зато наблюдаем торосы высотой в несколько метров, для образования которых только и хватило сил сжатия в ледовых полях, увлекаемых водными и воздушными течениями (к тому же, часто торосы образуются лишь после разгона ледяных полей на открытой воде при закрытии трещины), хотя толщина и прочность льдов в тысячи раз меньше толщины и прочности коры.
Прогнозирование.
Поскольку пластическая деформация коры (землетрясение) происходит в момент превышения предела прочности пород коры результирующей (суммарной) силой, то возможен прогноз времени землетрясения - времени превышения этого предела. Для вычисления прогноза землетрясения необходимо знать: а) текущие напряжения, б) текущий предел прочности, в) прогноз изменения напряжений, г) прогноз изменения прочности.
Воздействие медленно меняющихся главных движущих сил, создающих подавляющую часть (почти 100%) механического напряжения, может быть достаточно легко учтено (хотя бы путем экстраполяции). А вот воздействие намного меньших, но гораздо быстрее меняющихся по величине спусковых сил должно учитываться отдельно. Именно быстро меняющиеся спусковые силы (главные из них - силы атмосферного давления и приливные силы в зависимости от фазы Луны) определяют приход землетрясения с точностью до лет, дней, часов и минут. Тогда как гораздо большие, но медленно меняющиеся главные движущие силы определяют время прихода землетрясения с эпицентром в заданном месте с точностью до столетий и тысячелетий.
Для сильных землетрясений промежуток времени между двумя землетрясениями с эпицентром в одном и том же месте составляет сотни и тысячи лет. За это время механическое напряжение в коре вследствие действия главных сил монотонно вырастает от остаточного напряжения (остающегося от предыдущей разрядки - землетрясения) практически до предела прочности. За это время приливные (и другие) силы успевают измениться от ежедневного минимума до максимума сотни тысяч раз. И хотя амплитуда их изменения в сотни раз меньше амплитуды главных сил, абсолютные скорости их изменения в тысячи раз больше скоростей нарастания главных сил. Поэтому именно быстро меняющаяся добавка к главным силам (сумма спусковых сил) успевает сделать последнее усилие, приводящее к превышению предела прочности (представляет собой последнюю каплю, переполняющую чашу).
Приливные силы изменяются от минимума до максимума дважды в сутки (с полным циклом изменения амплитуды в ![]() месяца). Но, вопреки распространенному мнению, они являются не единственной спусковой силой. Более того, они не являются даже главной спусковой силой (особенно в высоких широтах, где приливы малы). Об этом говорит сопоставление фаз Луны и моментов прихода землетрясений.
месяца). Но, вопреки распространенному мнению, они являются не единственной спусковой силой. Более того, они не являются даже главной спусковой силой (особенно в высоких широтах, где приливы малы). Об этом говорит сопоставление фаз Луны и моментов прихода землетрясений.
На секторы новолуния и полнолуния (когда приливы максимальны) приходится в разных выборках 56% - 65% землетрясений, тогда как на секторы первой и третьей четверти Луны (равные по длительности новолунию и полнолунию) приходится, соответственно, 44% - 35% [2]. Эти цифры (65% для катастрофических землетрясений) говорят о несомненной корреляции времени землетрясения и фазы Луны. Но из этих же цифр видно также, что существуют и другие, не менее действенные спусковые силы.
По нашему мнению, главной спусковой силой является быстро меняющаяся сила атмосферного давления. Действительно, вполне возможное изменение атмосферного давления на 3% (23 мм р. ст.) по своему воздействию на земную кору эквивалентно появлению или исчезновению на огромном участке земной поверхности слоя воды толщиной в 30 см, или гранитного слоя толщиной в 10 см. И такие изменения происходят за единицы часов! Тогда как изменение главных сил на такую же величину происходит за сотни лет (100 мм = сотни лет * 1 мм/год, [2]). Поэтому в краткосрочном прогнозе землетрясений, кроме знания текущих напряжений и предела прочности, решающую роль должен играть прогноз погоды в части распределения атмосферного давления по земной поверхности вместе с учетом фазы прилива. Понятно, что повышенное атмосферное давление над участком коры, который опустится в результате землетрясения вниз, и пониженное над поднимающимся участком будет способствовать приходу землетрясения. Точно так же землетрясение может быть спровоцировано добавочной горизонтальной силой трения воздушных потоков - ветров в нужных направлениях. Именно воздействием атмосферных явлений может быть объяснена наблюдаемая корреляция частоты землетрясений и активности Солнца - активизация Солнца вызывает активизацию атмосферных явлений на Земле (увеличение амплитуды перепадов давления), которые и провоцируют большее количество землетрясений.
Но для окончательного доказательства действенности сил атмосферного давления необходимо провести детальный анализ решений больших землетрясений и глобальных синоптических карт на моменты этих землетрясений. А также синоптических карт на моменты начал извержений различных вулканов (поскольку извержение вулкана является частным, довольно редким, случаем плавного, медленно протекающего землетрясения - пластической деформации земной коры с выдавливанием магмы из замкнутого объема магматического очага).