Реферат: Графическое представление данных в статистике

Рассмотрим построение фигурной диаграммы по данным табл. 5.4 фермерских хозяйств в России за 1993-1995 гг.

Таблица 5.4

Численность фермерских хозяйств в России за 1993 - 1995 гг.

(данные условные) (тыс.)

Год	1993	1994	1995
Численность фермерских хозяйств	49	183	270

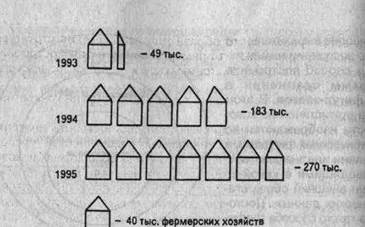
Рис. 5.15. Динамика численности фермерских хозяйств в одном из регионов России за 1993-1995 гг.

Примем условно за один знак 40 тыс. фермерских хозяйств. Тог­да число хозяйств в России в 1993 г. в размере 49 тыс. будет изображено в количестве 1,22 хозяйства, в 1994 г. - 4,6 хозяйства и т. д. (рис. 5.15).

Как правило, фигурные диаграммы широко используются для популяризации статистических данных и рекламы.

5.4. СТРУКТУРНЫЕ ДИАГРАММЫ

Основное назначение структурных диаграмм заключается в графическом представлении состава статистических совокупностей, характеризующихся как соотношение различных частей каждой из совокупностей. Состав статистической совокупности графически может быть представлен с помощью как абсолют­ных, так и относительных показателей. В первом случае не толь­ко размеры отдельных частей, но и размер графика в целом определяются статистическими величинами и изменяются в соответствии с изменениями последних. Во втором - размер всего графика не меняется (так как сумма всех частей любой совокупности составляет 100%), а меняются только размеры отдельных его частей. Графическое изображение состава сово­купности по абсолютным и относительным показателям способ­ствует проведению более глубокого анализа и позволяет про­водить международные сопоставления и сравнения социально-экономических явлений.

В качестве графического образа для изображения структуры совокупностей применяются прямоугольники - для построения столбиковых и полосовых диаграмм и круги -для построения сек­торных диаграмм.

Покажем построение указанных выше диаграмм на конкретных примерах.

Чтобы по приведенным данным табл. 5.5 построить диаграм­му, отражающую структуру сравниваемых совокупностей по соот­ношению в них отдельных видов часов, ряд абсолютных показа­телей заменяется рядом относительных величин. В этом случае каждая из полос диаграммы будет иметь одинаковую длину, так как при переходе к относительным величинам погашаются различия в абсолютных размерах совокупностей. В то же время структур­ные различия проявляются значительно четче. Графическое изоб­ражение структуры с помощью столбиковых (полосовых) диаграмм позволяет изучить особенности многих изучаемых экономических явлений. Так, приведенная на рис. 5.16 диаграмма, построенная по данным табл. 5.5, характеризует увеличение доли наручных часов в общем производстве.

Таблица 5.5

Производство часов по видам в одном из регионов России за 1985 - 1995 гг.

	198	5г.	199	5г.
	млн. шт.	%	млн. шт.	%
Часы, всего	52,5	100,0	60,1	100,0
В том числе:
наручные настенные	24,4 9,3	46,5 17,7	31,6 10,5	52,6 17,5
будильники	18,8	35,8	18,0	29,9

Более распространенным способом графического изображе­ния структуры статистических совокупностей является секторная Диаграмма, которая считается основной формой диаграммы та­кого назначения. Это объясняется тем, что идея целого очень хорошо и наглядно выражается кругом, который представляет всю совокупность. Удельный вес каждой части совокупности в сектор­ной диаграмме характеризуется величиной центрального угла (угол между радиусами круга). Сумма всех углов круга, равная 360°, приравнивается к 100%, а следовательно, 1% принимает­ся равным 3,6°.

Рис. 5.16. Динамика удельного веса производства часов по видам (1985-1995 гг.)

Приведем пример построения секторной диаграммы по данным табл. 5.6.

Таблица 5.6

Динамика доли негосударственного сектора экономики в розничной торговле (в % к общему объему розничного товарооборота в России)

	---1--————-Г' 1992г.	»,а о г Ч01.ИИ/ 1993 г.
Государственный сектор Негосударственный сектор	78 22	49
В том числе предприятия:		51
частной и смешанной форм
собственности
потребительской кооперации прочих форм собственности	1,8 20 0,2	31 16 4

Построение секторной диаграммы начинается с определения центральных углов секторов. Для этого процентное выражение от­дельных частей совокупностей умножают на 3,6°. Например, для данных:

1992г.: 78 • 3,6° = 280,8°; 1,8 • 3,6° = 6,5°; 20 • 3,6° = 72°;

0,2 • 3,6° = 0,7°;

1993г.: 49-3,6° =176,4°; 31-3,6° = 111,6°; 16 • 3,6° = 57,6°;

4 • 3,6° = 14,4°.

Рис. 5.17. Динамика доли негосударственного сектора экономики в розничной торговле (в % к общему объему розничного товарооборота в России)

По найденным значениям углов круги делятся на соответству­ющие секторы (рис. 5.17).

Применение секторных диаграмм позволяет не только графи­чески изобразить структуру совокупности и ее изменение, но и по­казать динамику численности этой совокупности. Для этого стро­ятся круги, пропорциональные объему изучаемого признака, а за­тем секторами выделяются его отдельные части.

Рассмотренные способы графического изображения структуры совокупности имеют как достоинства, так и недостатки.

Так, секторная диаграмма сохраняет наглядность и выразитель­ность лишь при небольшом числе частей совокупности, в против­ном случае ее применение малоэффективно. Кроме того, нагляд­ность секторной диаграммы снижается при незначительных изме­нениях структуры изображаемых совокупностей: она выше, если имеются существенные различия сравниваемых структур. Преиму­ществом столбиковых (ленточных) структурных диаграмм по срав­нению с секторными являются их большая емкость, возможность отразить более широкий объем полезной информации.

5.5. ДИАГРАММЫ ДИНАМИКИ

Для изображения и внесения суждений о развитии явления во времени строятся диаграммы динамики.

Для наглядного изображения явлений в рядах динамики ис­пользуются диаграммы: столбиковые, ленточные, квадратные, круговые, линейные, радиальные и др. Выбор вида диаграммы зависит в основном от особенностей исходных данных, цели ис­следования. Например, если имеется ряд динамики с несколь­кими неравноотстоящими уровнями во времени (1913, 1940, 1950, 1980, 1985, 1997 гг.), то часто для наглядности используют стол­биковые, квадратные или круговые диаграммы. Они зрительно впечатляют, хорошо запоминаются, но не годны для изображе­ния большого числа уровней, так как громоздки. Когда число уров­ней в ряду динамики велико, целесообразно применять линей­ные диаграммы, которые воспроизводят непрерывность процес­са развития в виде непрерывной ломаной линии. Кроме того, линейные диаграммы удобно использовать: если целью иссле­дования является изображение общей тенденции и характера развития явления; когда на одном графике необходимо изобра­зить несколько динамических рядов с целью их сравнения; если наиболее существенным является сопоставление темпов роста, а не уровней.

Для построения линейных графиков применяют систему пря­моугольных координат. Обычно по оси абсцисс откладывается время (годы, месяцы и т. д. ), а по оси ординат - размеры изоб­ражаемых явлений или процессов. На оси ординат наносят мас­штабы. Особое внимание следует обратить на их выбор, так как от этого зависит общий вид графика. Обеспечение равновесия, пропорциональности между осями координат необходимо в гра­фике в связи с тем, что нарушение равновесия между осями ко­ординат дает неправильное изображение развития явления;

Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебания в дина­мике явлений мало выделяются, и наоборот, преувеличение масштаба по оси ординат по сравнению с масштабом на оси абсцисс дает резкие колебания. Равным периодам времени и размерам уровня должны соответствовать равные отрезки мас­штабной шкалы.

В статистической практике чаще всего применяются графичес­кие изображения с равномерными шкалами. По оси абсцисс они берутся пропорционально числу периодов времени, а по оси ор­динат - пропорционально самим уровням. Масштабом равномер­ной шкалы будет длина отрезка, принятого за единицу.

рассмотрим построение линейной диаграммы на основании следующих данных (табл. 5.7).

Таблица 5.7

Динамика валового сбора зерновых культур в регионе за 1985-1994 гг.

Год	1985	1986	1987	1988	1989	1990	1991	1992	1993	1994
Млн.т	237,4	179,2	189,1	158,2	186,8	192,2	172,6	191,7	210,1	211,3

Изображение динамики валового сбора зерновых культур на координатной сетке с неразрывной шкалой значений, начинающих­ся от нуля, вряд ли целесообразно, так как 2/3 поля диаграммы остаются неиспользованными и ничего не дают для выразитель­ности изображения. Поэтому в данных условиях рекомендуется строить шкалу без вертикального нуля, т. е. шкала значений раз­рывается недалеко от нулевой линии и на диаграмму попадает лишь часть всего возможного поля графика. Это не приводит к искажениям в изображении динамики явления, и процесс его из­менения рисуется диаграммой более четко (рис. 5.18).

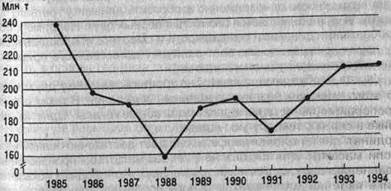
Рис. 5.18. Динамика валового сбора зерновых культур в регионе за 1985-1994 гг.

Нередко на одном линейном графике приводится несколько кри­вых, которые дают сравнительную характеристику динамики раз­личных показателей или одного и того же показателя.

Примером графического изображения сразу нескольких показа­телей является рис. 5.19.

141

Рис. 5.19. Динамика производства чугуна и готового проката в регионе за 1985-1994 гг.

Однако на одном графике не следует помещать более трех-че­тырех кривых, так как большое их количество неизбежно ослож­няет чертеж и линейная диаграмма теряет наглядность.

В некоторых случаях нанесения на один график двух кривых дает возможность одновременно изобразить динамику третьего по­казателя, если он является разностью первых двух. Например, при изображении динамики рождаемости и смертности площадь меж­ду двумя кривыми показывает величину естественного прироста или естественной убыли населения.