Реферат: Графы. Решение практических задач с использованием графов (С++)

Это число можно представить в виде суммы: Г=φ1+φ2+φ3+…, где φ3 – число граней, ограниченных тремя ребрами, φ4 — число граней, ограниченных четырьмя ребрами и т. д.

С другой стороны, каждое ребро является границей двух граней, а поэтому число граней равно 2Р, в то же время 2Р=20=3φ3+4φ4+... . Умножив равенство Г=7=φ3+ φ4 + φ5 + … на три, получим ЗГ=21=3( φ3 + φ4 + φ5 + …).

Ясно, что (3φ3+3φ4+3φ5+…) < (3φ3+4φ4+ 5φ5+…) или 3Г<2Р, но по условию, 2Р=20, а ЗГ=21; поэтому вывод, полученный при введенном нами предположении (граф плоский), противоречит условию. Отсюда заключаем, что полный граф с пятью вершинами не является плоским.

Теорема 11. (Теорема Понтрягина-Куратовского) Граф является плоским тогда и только тогда, когда он не имеет в качестве подграфа полного графа с пятью вершинами.

В заключение этого параграфа, на наш взгляд, следует упомянуть то, что в нем объяснялись только основные теоремы теории графов. Их практическое применение будет рассмотрено в следующих параграфах реферата.

Способы представления графов в компьютере

Конструирование структур данных для представления в программе объектов математической модели – это основа искусства практического программирования. Далее приводится четыре различных базовых представления графов. Выбор наилучшего представления определяется требованиями конкретной задачи. Более того, при решении конкретных задач используются, как правило, некоторые комбинации или модификации указанных представлений, общее число которых необозримо. Но все они так или иначе основаны на тех базовых идеях, которые описаны в этом разделе.

Требования к представлению графов

Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Далее приведены четыре наиболее часто используемых представления с указанием характеристики n(p,q) – объема памяти для каждого представления. Здесь p – число вершин, а q – число ребер.

Матрица смежности

Представление графа с помощью квадратной булевой матрицы M, отражающей смежность вершин, называется матрицей смежности, где

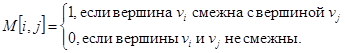
Для матрицы смежности n(p,q) = O(p2).

Замечание

Матрица смежности неориентированного графа симметрична относительно главной диагонали, поэтому достаточно хранить только верхнюю (или нижнюю) треугольную матрицу.

Матрица инциденций

Представление графа с помощью матрицы H, отражающей инцидентность вершин и ребер, называется матрицей инциденций, где для неориентированного графа

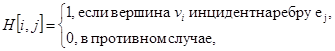
а для орграфа

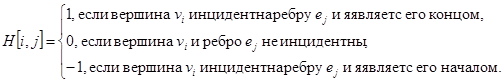
Для матрицы инциденций n(p,q) = O(pq).

Списки смежности

Представление графа с помощью списочной структуры, отражающей смежность вершин и состоящей из массива указателей на списки смежных вершин, где элемент списка представлен структурой

N : record v : 1..p; n :↑ N end record,

называется списком смежности. В случае представления неориентированных графов списками смежности n(p,q) = O(p+2q), а в случае ориентированных графов n(p,q) = O(p+q).

Массив дуг

Представление графа с помощью массива структур

E : array [1..q] of record b,e : 1..p end record,

отражающего список пар смежных вершин, называется массивом ребер (или, для орграфов, массивом дуг). Для массива ребер (или дуг) n(p,q) = O(2q).