Реферат: Индексные числа
Существует три способа выбора весов. Первый использует объем потребления продукции в течение базового периода при подсчете каждого индексного числа. Этот метод называется методом Ласпере (по имени автора метода). Второй использует количество потребляемой продукции в течение рассматриваемого периода (для каждого индексного числа). Это метод Пааше. Третий способ назван совокупным методом фиксированных весов. В этом случае выбирается один период и его количественные характеристики используются для нахождения всех индексов. (Заметим, что, если выбранный период - базовый, то данный метод сводится к методу Ласпере.
Метод Ласпере.
Метод Ласпере, в котором используется объем потребления продукции за базовый период, применяется наиболее широко, т.к. в нем используется количественные характеристики лишь для данного периода. Менеджеры так же могут непосредственно сравнивать индекс одного периода с другим, поскольку каждое индексное число зависит от одной и той же базовой цены и количества. Предположим, что ценовой индекс производства стали составлял 103 в 1986 г. и 125 в 1989 г. Используя базовые цены и объем потребления продукции в 1986 г., компания сделала вывод, что общий уровень цен вырос на 22% с 1986 по 1989 гг. Для подсчета индекса Ласпере сначала цена в текущем периоде умножается на количество в базовом периоде (для каждого элемента группы), затем результирующие значения суммируются. Та же процедура выполняется для базового периода (цена каждого элемента умножается на количество, затем производится суммирование полученных чисел). Поделив первую сумму на вторую и умножив результат на 100, получаем значение индекса Ласпере. Формула подсчета индекса Ласпере:
 *100, (3.3) где
*100, (3.3) где
Q 0 - объем продаж в базовый период;
P1 - цены в текущем году;
P0 - цены в базовом году.
Пример: Предположим, что необходимо определить изменения в уровне цен между 1985 и 1989 гг. В табл. 3.7 приведено вычисление индекса Ласпере. Интерпретация вычисленного индекса: если мы имеем репрезентативную выборку товаров, то можно заключить, что общий ценовой индекс для 1989 г. составил 121 (при условии, что для 1985 г. - 100), или, что то же самое, цены выросли на 21%. Отметим, что мы использовали средний объем потребления товаров в 1985 г., а не совокупный объем потребления. В действительности это не играет большой роли, пока мы применяем одинаковые количественные характеристики в процессе вычисления индекса. Обычно выбирается наиболее простая количественная характеристика.
Таблица 3.7
Подсчет индекса Ласпере
Элементы совокупного индекса (1) | P0 Базовая цена 1985 г (долл.) (2) | P1 Текущая цена 1989 г. (долл.) (3 ) | Q0 Среднее количество продуктов, потребленных семьей в 1985 г. (4) | P0 Q0 (4)*(2) (долл.) (5) | P1 Q0 (3)*(4) (долл.) (6) |
Хлеб, бух. Картофель, фунт. Курица, шт. | 0.91 0.79 3.92 | 1.19 0.99 4.50 | 200 300 100 | 182 237 392 | 238 297 450 |
| S | 811 | 985 |
.
Ценовой индекс Ласпере =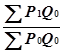 * 100 = 121
* 100 = 121
Преимущества метода Ласпере:
1) Возможность сравнивать один индекс с другим. Если бы в предыдущем примере у нас были бы цены 1986 г., то мы смогли бы найти значение общего ценового индекса для 1986 г. Этот индекс можно было бы непосредственно сравнивать с индексом для 1989 г. за счет использования одних и тех же базовых количеств.
2) Многие широко используемые количественные характеристики не вычисляются ежегодно. Фирму, например, может интересовал тот показатель, который подсчитывается один раз в 10 лет. И, поскольку метод Ласпере использует только одну переменнуюQ0 (относящуюся к базовому году), то фирме нет необходимости искать ежегодные значения для подсчета количественной характеристики.
Главный недостаток метода Ласпере: Он не учитывает изменения в структуре потребления. Продукция, пользовавшаяся большим спросом всего несколько лет назад, может оказаться совершенно невостребованной сегодня. Если количественные характеристики базового года значительно отличаются от характеристик рассматриваемого периода, то изменение цены на эту продукцию плохо характеризует изменение общего уровня цен.
Метод Пааше
Нахождение индекса Пааше сходно с нахождением индекса Ласпере. Различие "Заключается в том, что в методе Пааше используется количественная мера для текущего периода, как в методе Ласпере. Последовательность вычислений:
1) Цена текущего периода умножается на количество каждого товара из группы в текущем периоде. Результаты складываются.
2) Цена базового периода умножается на количество каждого товара в текущем периоде. Результаты складываются.
3) Первая сумма делится на вторую, а результат умножается на 100 для представления индекса в виде процента.
Индекс Пааше =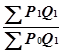 * 100, (3.4) где
* 100, (3.4) где
P1 - цена текущего периода;
P0 - цена базового периода;
Q1 - Количественные характеристики текущего периода.
Используя эту формулу, мы можем пересмотреть расчеты в табл.3. 7 . Заменим количество потребленной продукции для 1985 г. на данные 1989 г. В табл.3.8 представлены новые вычисления для этой задачи.
Таблица 3.8
Подсчет индекса Пааше
Элементы совокупного индекса (1) | P0 Базовая цена 1985 г (долл.) (2) | P1 Текущая цена 1989 г. (долл.)(3 ) | Q1 Среднее количество продуктов, потребленных семьей в 1989 г.(4) | P0 Q1 (4)*(2) (долл.) (5) | P1 Q1 (3)*(4) (долл.) (6) |
Хлеб, бух. Картофель, фунт. Курица, шт. | 0.91 0.79 3.92 | 1.19 0.99 4.50 | 200 100 300 | 238 99 1350 | 182 79 1176 |
| S | 1687 | 1437 |
Ценовой индекс Пааше =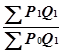 * 100 = 117
* 100 = 117
Интерпретация различий между двумя методами. В данном случае мы определили, что ценовой индекс для 1989 г. составил 117, а индекс Ласпере равнялся 121 (табл.3. 7 ). Разница в этих индексах отражает изменения в структуре потребления (для трех элементов данной группы).
Преимущества метода Пааше: Этот метод наиболее точен, так как в нем учитываются эффекты изменения в цене и структуре потребления. Следовательно, он лучше отображает изменения в экономике, чем индекс Ласпере. В нашем примере метод Пааше характеризует склонность к менее дорогим товарам и услугам, так как он показывает увеличение уровня цен на 17%, а не на 21% (согласно методу Ласпере).
Недостатки: Этот метод неудобен тем, что необходимо вычислять количественные характеристики для каждого рассматриваемого периода. Часто подобного рода информация недоступна, или ее получение сопряжено с большими затратами. Например, трудно найти надежный источник информации о годовом объеме потребления 100 пищевых продуктов в различных странах в течении нескольких лет. Значение ценового индекса Пааше есть результат как ценовых, так иколичественных изменений относительно базового периода. Поскольку количественные характеристики, используемые для одного индексного периода, часто отличаются то характеристик другого индексного периода, то становится невозможным объяснить различия между индексами, вычисленными для этих периодов, только изменением уровня цен. Поэтому трудно сравнивать индексы Пааше, полученные для разных периодов времени.
Точный ценовой индекс (индекс Глушенкова) .
Ранее говорилось, что при подсчете индекса некоторым переменным следует приписывать большую важность чем другим. В ценовых индексах весом мы выбирали потребленной продукции. Мы показываем каково значение данного товара на ценовой индекс в зависимости от количества его продаж и потребления, т.е. наиболее употребляемые товары и будут оказывать наибольшее воздействие на ценовой индекс. Но выбирая в качестве веса количество потребленной продукции в течении рассматриваемого или базового периода не учитывается, что вкусы людей меняются и соответственно значение переменных в различных периодах - различно. Чтобы избавиться от этого недостатка нужно присваивать переменным рассматриваемого и базового периода свои веса (в данном случае количество потребленной продукции). Формула вычисления индекса будет иметь следующий вид:
Индекс=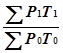 * 100, (3.5) где
* 100, (3.5) где
P1 - цена текущего периода;
P0 - цена базового периода;
T0 - вес продукции в базовом периоде;
T1 - вес продукции в текущем периоде.
Но следует учитывать объем потребленной продукции может меняться из-за роста населения. Рассмотрим табл. 3.9
Таблица 3.9
Подсчет ценового индекса
Элементы совокупного индекса (1) | P0 Базовая цена 1985 г (долл.) (2) | P1 Текущая цена 1989 г. (долл.) (3 ) | Q0 Среднее количество продуктов, потребленных семьей в 1985 г. (4) | Q1 Среднее количество продуктов, потребленных семьей в 1985 г. (5) | P0 Q0 (4)*(2) (долл.) (6) | P1 Q1 (3)*(5) (долл.) (7) |
Хлеб, бух. Картофель, фунт. Курица, шт. | 0.91 0.79 3.92 | 0.91 0.79 3.92 | 200 300 100 | 300 450 150 | 182 237 392 | 273 356 588 |
| S | 811 | 1217 |
Из таблицы видно, что спрос на данные товары из-за роста населения или каких то других причин вырос в 1.5 раза. Так как цены остались прежними, то ценовой индекс должен быть равен 100. Если считать по формуле (3.5) :
Индекс=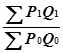 * 100=
* 100=![]() *100 =150
*100 =150
Для избежания подобной ошибки следует брать в качестве веса не количество потребленной продукции, а отношение количества рассматриваемой потребленной продукции ко всему количеству потребленной продукции за указанный период:
Индекс=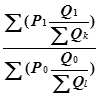 * 100, (3.6) где
* 100, (3.6) где
P1 - цена текущего периода;
P0 - цена базового периода;
Q0 - количество потребленной продукции;
Q1 - количество потребленной продукции в;
S Ql - количество всей рассматриваемой продукции потребленной в базовом периоде;
S Qk - количество всей рассматриваемой продукции потребленной в текущем периоде.
Рассмотрим тот же самый пример по формуле (3.6) с помощью таблиц 3.10 .
Таблица 3. 10
Подсчет ценового индекса
Элементы совокупного индекса (1) | P0 Базовая цена 1985 г (долл.) (2) | P1 Текущая цена 1989 г. (долл.) (3 ) | Q0 Среднее количество продуктов, потребленных семьей в 1985 г. (4) | Q1 Среднее количество продуктов, потребленных семьей в 1985 г. (5) | Q0 / S Ql ( S (4) ) /(2) (долл.) (6) | Q1 / S Qk ( S (3) ) /(5) (долл.) (7) |
Хлеб, бух. Картофель, фунт. Курица, шт. | 0.91 0.79 3.92 | 0.91 0.79 3.92 | 200 300 100 | 300 450 150 | 0.333 0.500 0.167 | 0.333 0.500 0.167 |
| S | 600 | 900 |
Индекс=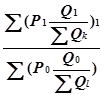 * 100 =
* 100 =![]()
По сравнению с предыдущими методами данный метод обладает наибольшей точностью, но в данном случае необходимо знать цены и количество потребленной продукции как за базовый период, так и за рассматриваемый.
Совокупный метод взвешенных весов (СМВВ)
Совокупный метод взвешенных весов - третий способ приписывать веса элементам группы. Он схож и с первым, и со вторым методами. Однако в отличие от первых двух, он использует количественные характеристики репрезентативного периода. Репрезентативные веса называются фиксированными. Фиксированные веса и базовые цены не обязательно относятся к одному и тому же периоду времени.
Подсчет индекса
Данный индекс вычисляется следующим образом:цены текущего периода умножаются на фиксированные веса, и результаты суммируются. Затем цены базового периода умножаются на фиксированные веса, и результаты так же суммируются. Затем мы делим первую сумму на вторую и умножаем полученный результат на 100 для представления отношения в виде процента.
СМВВ=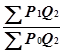 *100, (3.7) где
*100, (3.7) где
P1 - цены текущего периода;
P0 - цены базового периода;
Q2 - Фиксированные веса.
Пример: Машиностроительной компании необходимо определить изменения в ценах напоставляемое сырье за период с 1969 по 1989 гг. Данные для вычисления индекса представлены в табл.3.11. Исследование объемов закупок сырья в течении этого периода показало, что данные за 1982 г. наилучшим образом отражают структуру закупок сырья за все 20 лет. Уровень цен 1969 г. в данном примере является базовым. Расчеты показывают, что за 20 лет рост цен на сырье составил 157%.
ТаблицаЗ. 11
Подсчет совокупного индекса взвешенных весов
| Вид сырья | Q2 Объем. | P0 | P1 | P0 Q2 | P1 Q2 |
| потребл в 1982г. (тыс.т) | Средняя цена долл. за тонну | (3)*(2) | (4)*(2) | ||
| (1) | . (2) | 1984 г. (3) | 1989 г. (4) | (5) | (6) |
Уголь Железная руда Никель | 158 12 5 | 7.56 9.20 12.30 | 19.50 21.40 36.10 | 1194.48 110.40 61.50 | 3081.80 256.80 180.50 |
| S Q2 Pi | 1366.38 | 3518.30 | |||
Индекс = 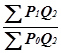 *100=257
*100=257
Преимущества совокупного метода фиксированных весов.
Основное преимущество данного це?