Реферат: Информационный процесс. Обработка информации

1) известен вид функции s(t) и известно, что она не равна нулю на интервале времени (tн,tк),

2) известна статистика помехи (например, плотность вероятности ее амплитуды).

В приемнике решается, был ли передай сигнал на интервале времени (tн,tк) или нет. Очевидно, что решение нельзя принять до наступления момента времени tн, а в ряде случаев – и до наступления момента tк. Приемник анализирует сигнал x(t) на интервале (tн,tк) и в некоторый момент времени t0³tк должен выдать решение.

Рассмотрим решение данной задачи при следующих ограничениях (условиях):

1) известен вид сигнала s(t), действующего в интервале времени (0, t0);

2) помеха n(t) является аддитивной и представляет собой белый шум, т.е. спектральная плотность мощности помехи Gn(f)=C, где – постоянная величина.

Приемник является линейной системой, к которой применим принцип суперпозиции. На вход приемника поступает воздействие, представляющее собой смесь полезного сигнала s(t) и помехи n(t): x(t)=s(t)+n(t).

Реакцию такой системы на это входное воздействие можно представить как сумму p(t)=x(t)+e(t), где x(t) – реакция системы, вызванная воздействием полезного сигнала s(t); e(t) – результат преобразования системой помехи n(t). Такое разделение произвести можно, если приемник – линейная система.

Помеху, действующую в канале связи, практически нельзя уменьшить, поэтому для повышения помехоустойчивости и пропускной способности канала связи стремятся обычно увеличить мощность полезного сигнала s(t). Как правило, выбирают максимально возможную мощность, учитывая ограничения, накладываемые аппаратурой и самой линией связи, чтобы обеспечить максимальное отношение Pc/sn2, где Pc – мощность полезного сигнала, а sn2 – мощность помехи, отнесенные к входу приемника

Функция приемника – обработать сигнал, чтобы еще больше увеличить отношение сигнал/помеха. Рассмотрим задачу обнаружения сигнала на фоне помех как задачу синтеза линейного фильтра, на выходе которого в момент времени t0 имеет место максимум отношении x(t0)/se2, где se2 – мощность (дисперсия) помехи на выходе фильтра.

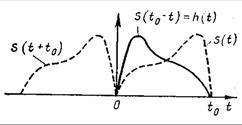
Рис. 3.1. Импульсная характеристика линейного фильтра

(3.6)

?????? ??????? ??????????? ? ?????????? ???? ??? ????????? ?????????????? W(jf), ???? ??? ?????????? ?????????????? h(t). ??? ???? ??????????, ????? ??????????? ???????

min[-2kx(t0)],

где k – произвольный постоянный коэффициент.

Учитывая, что спектр помехи e(t) на выходе фильтра зависит от его частотной характеристики:

,

определим мощность помехи:

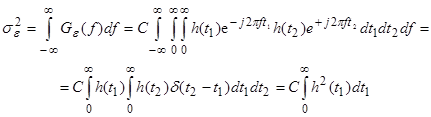
Выходной сигнал фильтра в момент времени t0

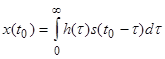
Преобразуем выражение (3.6):

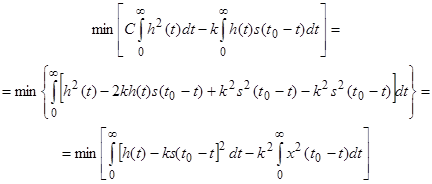
Интеграл 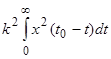представляет собой энергию сигнала и при заданной функции s(t) является постоянной величиной. Условием минимума является равенство нулю интеграла 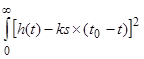, т.е. .

Это условие эквивалентно равенству , означающему, что наибольшее отношение сигнал/помеха в момент времени t0 на выходе фильтра достигается тогда, когда импульсная характеристика фильтра является зеркальным отображением полезного сигнала s(t+t0) (рис. 3.1).

Сжатие и адаптивная дискретизация сигналов

Рассмотрим источники измерительной информации и измерительные сигналы. В качестве источников измерительной информации выступают физические объекты разнообразной природы. Для отбора измерительной информации используются различные измерительные преобразователи, основная функция которых состоит в превращении контролируемого параметра или параметров объекта измерения в сигналы. Поэтому ряд свойств измерительных сигналов определяются как видом объекта измерения, так и условиями измерения.

В измерительной технике актуальна проблема обработки больших потоков измерительной информации. Решая эту проблему, можно пойти двумя путями: увеличивать быстродействие средств обработки информации или же сократить объемы обрабатываемой информации.

Быстродействие средств обработки информации (ЭВМ, микропроцессоров) определяется уровнем развития науки и технологии, и путь, связанный с увеличением быстродействия, не обеспечивает быстрого решения проблемы. А вот сократить объем обрабатываемой измерительной информации во многих случаях можно. Взять хотя бы такой пример: испытывается серийный тип самолета. При этом из предыдущих испытаний самолетов того же типа достаточно подробно известны его важнейшие параметры. В этом случае нет необходимости передавать и обрабатывать параметры, пока они находятся в норме. Но если тот или иной параметр существенно отклонился от нормы, то его необходимо передавать и обрабатывать. Такой подход позволяет иногда во много раз сокращать объем обрабатываемой измерительной информации и время ее обработки.

Измерительные сигналы могут содержать избыточную информацию. Если устранить из измерительных сигналов избыточную информацию, можно повысить эффективность обработки измерительной информации.

Устранение избыточности информации измерительных сигналов получило название сжатия измерительных сигналов.