Реферат: Интегральное исчисление. Исторический очерк
Поясним сказанное одним примером.
Ньютон и Лейбниц разработали две трактовки понятия обычного определенного интеграла.
Ньютон трактовал определенный интеграл как разность соответствующих значений первообразной функции:
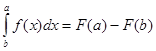 ,
,
где F`(x)=f(x).
Для Лейбница определенный интеграл был суммой всех бесконечно малых дифференциалов.
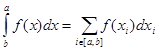 .
.
Первая трактовка отвечала технике вычисления определенных интегралов при помощи первообразной подынтегральной функции, вторая - потому, что в приложениях определенный интеграл появлялся как предел известного вида суммы (интегральной суммы).
Примерно до последней четверти XVIII века первая трактовка понятия определенного интеграла занимала господствующее положение. Этому способствовали два обстоятельства.
К началу XVIII века были установлены правила дифференцирования всех элементарных функций и началась успешная разработка методов нахождения их первообразных (рациональных, отдельных классов иррациональных и трансцендентных функций). Благодаря этому точка зрения Ньютона вполне отвечала развитию эффективных алгоритмов интегрального исчисления.
Непосредственное вычисление 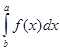 как предела интегральной суммы столкнулось с многими трудностями. Естественно, что это обстоятельство укреплению точки зрения Лейбница не способствовало.
как предела интегральной суммы столкнулось с многими трудностями. Естественно, что это обстоятельство укреплению точки зрения Лейбница не способствовало.
Истолкование обычного определенного интеграла по Лейбницу опиралось на понятие о бесконечно малых, от которого математики XVIII века хотели освободить математический анализ. Это также способствовало укреплению точки зрения Ньютона. Факт этот хорошо подтверждался тем, как Леонард Эйлер использовал понятие об интегральной сумме. Эйлер не возражал против приближенного вычисления определенных интегралов при помощи соответствующих интегральных сумм. Но рассматривать определенный интеграл как предел интегральной суммы он не мог. В этом случае все слагаемые интегральной суммы становились бесконечно малыми, т. е., с точки зрения Эйлера, были нулями.
Историческая справка. В 1963 г. 23-летний Пауль Эйлер окончил курс теологии в Базельском университете. Но учёных теологов было в те годы больше, чем требовалось, и лишь в 1701 г. он получил официальную должность священника сиротского дома в Базеле. 19 апреля 1706 г. пастор Пауль Эйлер женился на дочери священника. А 15 апреля 1707 г. у них родился сын, названный Леонардом.
Начальное обучение будущий учёный прошел дома под руководством отца, учившегося некогда математике у Якоба Бернулли. Добрый пастор готовил старшего сына к духовной карьере, однако занимался с ним и математикой – как в качестве развлечения, так и для развития логического мышления. Мальчик увлёкся математикой, стал задавать отцу вопросы один сложнее другого.
Когда у Леонардо проявился интерес к учёбе, его направили в Базельскую латинскую гимназию – под надзор бабушки.
20 октября 1720 г. 13-летний Леонард Эйлер стал студентом факультета искусств Базельского университета: отец желал, чтобы он стал священником. Но любовь к математике, блестящая память и отличная работоспособность сына изменили эти намерения и направили Леонарда по иному пути.
Став студентом, он легко усваивал учебные предметы, отдавая предпочтение математике. И немудрено, что способный мальчик вскоре обратил на себя внимание Бернулли. Он предложил юноше читать математические мемуары, а по субботам приходить к нему домой, чтобы совместно разбирать непонятное. В доме своего учителя Эйлер познакомился и подружился с сыновьями Бернулли – Николаем и Даниилом, также увлечённо занимавшимися математикой. А 8 июня 1724г. 17-летний Леонард Эйлер произнёс по- латыни великолепную речь о сравнении философских воззрений Декарта и Ньютона - и был удостоен учёной степени магистра (в XIX в. в большинстве университетов Западной Европы ученая степень магистра была заменена степенью доктора философии).
Эйлер отличался феноменальной работоспособностью. Он просто не мог не заниматься математикой или её приложениями. В 1735 г. Академия получила задание выполнить срочное и очень громоздкое астрономическое вычисление. Группа академиков просила на эту работу три месяца, а Эйлер взялся выполнить работу за 3 дня – и справился самостоятельно. Однако перенапряжение не прошло бесследно: он заболел и потерял зрение на правый глаз. Однако учёный отнёсся к несчастью с величайшим спокойствием: “Теперь я меньше буду отвлекаться от занятий математикой”, - философски заметил он.
До этого времени Эйлер был известен лишь узкому кругу учёных. Но двухтомное сочинение “ Механика, или наука о движении, в аналитическом изложении ”, изданное в 1736 г., принесло ему мировую славу. Эйлер блестяще применил методы математического анализа к решению проблем движения в пустоте и в сопротивляющейся среде. “Тот , кто имеет достаточные навыки в анализе, сможет всё увидеть с необычайной лёгкостью и без всякой помощи прочитает работу полностью”, - заканчивает Эйлер своё предисловие к книге.
Дух времени требовал аналитического пути развития точных наук, применения дифференциального и интегрального исчисления для описания физических явлений. Этот путь и начал прокладывать Леонард Эйлер.
Конечно, и до последней четверти XVIII века концепция Ньютона сталкивалась с трудностями. В этот период встречались элементарные функции, первообразные которых не могут быть выражены через элементарные функции. Знали математики и некоторые несобственные интегралы, в том числе и расходящиеся. Но такого рода факты были единичными и установившейся эффективной концепции интеграла нарушить не могли. Иным оказалось положение в последней четверти XVIII и особенно в начале XIX века.
С 70-х годов XVIII века решение задач аналитической механики, физики и других дисциплин потребовало значительное развитие понятия определенного интеграла. Особое значение приобретают двойные и тройные интегралы (Эйлер, Лагранж, Лаплас и др.).
Это было время, когда великие идеи Ньютона и Лейбница были опубликованы сравнительно недавно и современный математический анализ только создавался. Мощные методы, которые принесли с собой эти идеи, находили применение во всех отраслях точного знания. Применение это шло рука об руку с развитием самого анализа, часто указывая пути и направления, по которым должно развиваться новое исчисление. Это была, пожалуй, единственная по своей интенсивности эпоха математического творчества, и Эйлер был один из немногих по своей продуктивности творцов. Его "Введение в анализ бесконечно малых", "Основания дифференциального исчисления" и "Основания интегрального исчисления" были первыми трактатами, в которых уже обширный, но разрозненный материал нового анализа был объединен в цельную науку. В них был выработан тот скелет современного анализа, который сохранился и до нашего времени.
Разработка приемов вычисления двойных и тройных интегралов показала, что вычислять эти интегралы так, как вычисляли обычный определенный интеграл - при помощи неопределенного, очень трудно или даже невозможно. Поэтому математики вынуждены были сохранять концепцию Ньютона только на словах, а на деле, при решении задач точных наук, стали на путь Лейбница. Они вычисляли соответствующие интегральные суммы (в прямоугольных, цилиндрических и сферических координатах) и находили их пределы.
Короче говоря, разработка способов вычисления новых видов определенного интеграла показала, что обыкновенный, двойной и т. д. определенный интегралы должны быть обоснованы сами по себе независимо от понятия неопределенного интеграла. Но каждое слагаемое любой интегральной суммы является бесконечно малой величиной. Тем самым не только ставился вопрос о легализации ранее “изгоняемого” понятия бесконечно малого, но и о раскрытии его реального содержания и о соответствующем его использовании. Как уже указывалось, чтобы всё это сделать надо было преодолеть - обобщить, развить традиционное (Эйлерово) толкование функции и понятия предела.
В связи с этим возник вопрос о существовании пределов интегральных сумм, слагаемые которых были бы бесконечно малыми. В первой четверти XIX века понятие бесконечно малой оказалось необходимым и для изучения и сопоставления свойств непрерывных и разрывных функций. Получение основополагающих результатов связано здесь с именем Коши. “Между многими понятиями, - указывал Коши, - тесно связанными со свойствами бесконечно малых, следует поместить понятие о непрерывности и прерывности функций”. Тут же Коши дает истолкование непрерывности функции, которое более чем ясно подтверждает ясность этого его утверждения.
Новая постановка задач обоснования математического анализа ясно показывала, что дело не только в признании и применении бесконечно малых - это делали и раньше! - но прежде всего в научном истолковании их содержания и обоснованном на этом использовании их в алгоритмах математического анализа. Однако, чтобы это сделать надо было преодолеть господствовавшее в XVIII веке узкое толкование понятия предела, разработать общую теорию пределов.
Изучение разрывных функций и сопоставление их с функциями непрерывными заставило признать то, что ранее считалось невозможным: что предел, к которому стремиться последовательность значений функции, при стремлении аргумента в некоторой точке может оказаться отличным от значения функции в этой точке. Значит, предел не всегда является “последним” значением переменной, но во всех случаях предел есть число, к которому переменная приближается неограниченно. Следовательно, dx и dy не необходимо нули или “мистически” актуально бесконечно малые; бесконечно малая - это переменная, имеющая пределом нуль, причем факт этот с противоречиями и парадоксами не связан.
Коши преодолел и вторую ограничительную тенденцию в принятой до него трактовке понятия предела. Он признал, что переменная может приближаться к своему пределу не только монотонно, но и колеблясь, порой принимая значения, равные её пределу. Это обстоятельство придало теории Коши необходимую общность и исключительную гибкость. Мы до сих пор следуем пути, намеченному Огюстеном Луи Коши, с теми усовершенствованиями, которые были внесены во второй половине XIX века К. Вейерштрассом.