Реферат: Интегрирование методом Симпсона
Разработать алгоритм вычисления таблици значений
функции: у = S * cos(x) + q * sin(x),
где q - параметры функции,
S - значение интеграла.
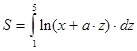
a=5
Интеграл вычислять с точностью EPS.
Вычислить N значений функции, начиная
с X=Xn и изменяя аргумент с шагом Dx.
Численное интегрирование функции одной переменной.
Численное интегрирование состоит в нахождении интеграла 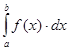 от непрерывной функции
от непрерывной функции ![]() по квадратной формуле:
по квадратной формуле:
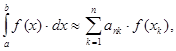
где коэффициенты ![]() - действительные числа и узлы
- действительные числа и узлы ![]() принадлежат
принадлежат ![]()
k=1, 2, ... , n. Вид суммы
![]()
определяет метод численного интегрирования, а разность

- погрешность метода.
Для метода Симпсона

![]() ,
, ![]()
![]() (k=1, 2, ..., 2n).
(k=1, 2, ..., 2n).
Правая часть формулы Симпсона является интегральной суммой и при ![]() стремится к данному интегралу. Однако при фиксированном h каждая из них отличаются от соответствующего интеграла на величину
стремится к данному интегралу. Однако при фиксированном h каждая из них отличаются от соответствующего интеграла на величину ![]() . По заданной предельной абсолютной погрешности
. По заданной предельной абсолютной погрешности ![]() подбирается параметр n, или, что то же самое, шаг h, при котором выполняется неравенство
подбирается параметр n, или, что то же самое, шаг h, при котором выполняется неравенство
![]()
Величина ![]() (в предположении существования входящих в них производных) характеризуется равенством:
(в предположении существования входящих в них производных) характеризуется равенством:
![]()
![]()
| начало Описание массивов X(100), Y(100) Ввод: a, q, EXP, Dx, XN, N, ZN, ZK
J = 1 X(J) = XN
XJ = X(J) S = INTEGR( a, XJ, EPS, ZN, ZK)
J = J + 1 --> ЧИТАТЬ ПОЛНОСТЬЮ <-- К-во Просмотров: 208
Бесплатно скачать Реферат: Интегрирование методом Симпсона
|


 Y(J) = S*cos( X(J) )+q*sin( X(J) )
Y(J) = S*cos( X(J) )+q*sin( X(J) )