Реферат: Исследование помехоустойчивого канала передачи данных методом имитационного моделирования на ЭВМ
выполнил:
студент 437 группы
Астраханцев Дима
проверил:
Безруков В.В.
Днепропетровск 2000
1. Исследование и выбор модели источника сообщений.
Для исследования информационных систем связи и управления обычно используют т.н. двоичные источники сообщений. Рачет ведется для независимых между собой сообщений. Хотя практически всегда имеет место такая зависимость, избыточность источника стараются устранить, повысив тем самым эффективность и надежность канала передачи данных (например, сжав или закодировав исходные сообщения). Алфавит двоичного источника состоит из двух сообщений (0 и 1) и поэтому его проще всего моделировать. В качестве источника независимых двоичных сообщений можно использовать т.н. квазислучайные последовательность (КСП), т.е. имеющие некоторый период повторений. Реализуемая практически каждой ЭВМ функция random дает КСП с очень большим периодом повторений, однако ее характеристики несколько уступают КСП сгенерированной с помощью т.н. регистра КСП.
Возмем, для сравнения, 9-ти элементный регистр (рисунок 1), длина периода КСП которого
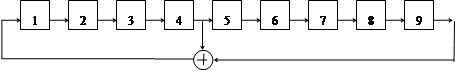 |
рисунок 1
составляет 29 =512 сообщения и стандартную функцию языка высокого уровня random(генератор случайных чисел - ГСЧ) как источники двоичных сообщений. Параметры источников занесем в таблицу 1 и сравним :
Таблица 1
| Параметр источника | Регистровый способ | Способ ГСЧ |
| Вероятностные характеристики КСП без учета зависимости между символами : | ||
| вероятность единицы | 0.50000 | 0.50586 |
| вероятность нуля | 0.50000 | 0.49414 |
| энтропия источника H, бит/символ | 1.00000 | 0.99990 |
| Вероятностные характеристики с учетом зависимости между символами : | ||
| условные вероятности единицы : p(1/1) | 0.50000 | 0.49421 |
| p(1/0) | 0.50000 | 0.51779 |
| условные вероятности нуля : p(0/1) | 0.50000 | 0.50579 |
| p(0/0) | 0.50000 | 0.48221 |
| финальная вероятность единицы: | 0.50000 | 0.50586 |
| финальная вероятность нуля: | 0.50000 | 0.49414 |
| условная энтропия "1" H1 , бит/символ | 1.00000 | 0.99990 |
| условная энтропия "0" H0 , бит/символ | 1.00000 | 0.99909 |
| энтропия источника H, бит/символ | 1.00000 | 0.99950 |
| Характеристики корреляционной функции : | ||
| значение КФ от нуля равно | 0.25000 | 0.24997 |
| эквивалентный интервал корреляции | 2.00000 | 4.00000 |
| среди боковых лепестков наибольший с номером | 61 | 2 |
| его величина составляет % от главного | 4.21286 | 15.28238 |
Как видно из таблицы, для моделирования случайного двоичного источника регистровый метод получения КСП предпочтительней т.к. выходная величина имеет характеристики случайной:
p(0)=p(1)=0.5 ; p(1/0)=p(0/0)=0.5; p(1/1)=p(0/1)=0.5;
![]() ,
, ![]()
H = p(0)H0 +p(1)H1 = 1 бит/символ.
О лучших случайных характеристиках можно также судить по графикам АКФ(рисунок 2) : квазислучайная последовательность полученная регистровым способом обладает лучшими корреляционными свойствами (малый размер боковых лепестков, большая удаленность максимального из боковых от нулевого).
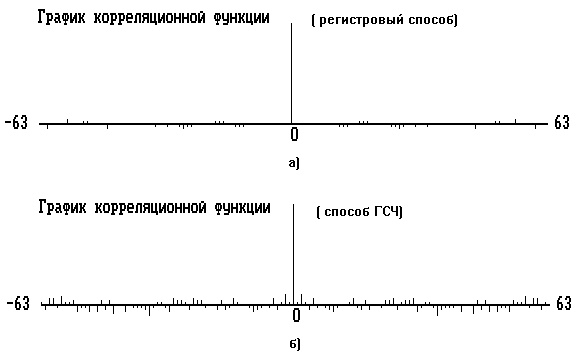
рисунок 2
Итак, в роли источника сообщений выбран регистр КСП, показаный на рисунке 1. Длина периода КСП - 512. Квазислучайная последовательность , в сокращенном виде : 00011110111000010....... 101111000001111111110.
2. Исследование линии на имитационной модели .
Характеристики канала очень важно знать для построения качественных систем передачи информации. В данном случае в роли канала выступает линия - симметричная пара кабеля типа ТПП, диаметром 0.4 мм и длиной 5 км. Естественно идеальным решением было бы измерение параметров уже существующей линии, но поскольку это довольно трудоемкая и длительная задача можно провести исследование на имитационной модели. В качестве такой модели можно выбрать аналитические выражения описывающие линию передачи (непрерывная модель линии), а можно использовать ее цифровой эквивалент (т.н. дискретная модель линии).
Передаточная функция аналоговой линии, представленной в виде колебательного звена:
![]() , где
, где
![]() - постоянная времени линии
- постоянная времени линии
![]() - коэффициент затухания линии.
- коэффициент затухания линии.
Если представить аналоговую линию в виде цифрового фильтра (рисунок 2), то используя Z-преобразование можно записать:
![]()
откуда выражение для выходного сигнала:
yn = a0 xn + a1 xn-1 + a2 xn-1 + b1 yn-1 + b2 yn-2 ,
где xn , yn - сигнал на входе и на выходе соответственно,
ai , bi - параметры, описывающие цифровую модель линии.
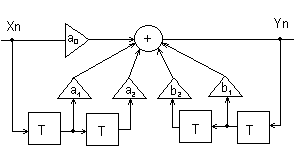
рисунок 3
С помощью такой модели можно исследовать различные характеристики системы, варьируя входными сигналами. Например при подачи на вход единичного ступенчатого импульса, на выходе имеем сигнал, соответствующий переходной характеристике линии.
С помощью программы «liniam» исследуем переходную и импульсную характеристики линии, амплитудно-частотную характеристику линии A(w) и частотную характеристику затухания a(w) . Задавая удельные значения L = 0.6 мГн/км, С=45 нФ/км, Rл = 280 Ом/км (для кабеля типа ТПП диаметром 0.4 мм) ,при сопротивлении нагрузки 600 Ом и принимая длину линии 5 км построим графики импульсной и переходной характеристики, АЧХ и ЧХ затухания (рисунок 3,4,5,6), приведя в таблице 2 численные значения этих характеристик.
Таблица 2
| N | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| t, с | 0 | 2.04e-6 | 4.08e-6 | 8.16e-6 | 1.42e-5 | 2.04e-5 | 3.88e-5 |
| ИХ g(t) | 0.584 | 1.000 | 0.693 | 0.331 | 0.112 | 0.037 | 0.001 |
| ПХ h(t) | 0.152 | 0.413 | 0.593 | 0.805 | 0.935 | 0.978 | 0.999 |
|
f, Гц |
--> ЧИТАТЬ ПОЛНОСТЬЮ <-- К-во Просмотров: 433
Бесплатно скачать Реферат: Исследование помехоустойчивого канала передачи данных методом имитационного моделирования на ЭВМ
|