Реферат: Избыточные коды

Московский Технический Университет Связи и Информатики

Кафедра Радиотехнических Систем

реферат по

избыточным кодам

Преподаватель: Смердова Н. Е.

Группа: РТ 9505

Студент: Матвеев А. Н.

Дата сдачи: Май 1999 года.

Москва, 1999 г.

Вступление.

Известно, что каналы, по которым передается информация, практически никогда не бывают идеальными (каналами без помех). В них почти всегда присутствуют помехи. Отличие лишь в уровне помех и их спектральном составе. Помехи в каналах образуются по различным причинам, но результат воздействия их на передаваемую информацию всегда один – информация теряется (искажается).

Для предотвращения потерь информации в канале были придуманы избыточные коды (коды с избыточностью). Преимущество избыточного кода в том, что при приеме его с искажением (количество искаженных символов зависит от степени избыточности и структуры кода) информация может быть восстановлена на приемнике.

Существуют избыточные коды с обнаружением (они только обнаруживают ошибку) и коды с исправлением (эти коды обнаруживают место ошибки и исправляют ее).

Для различных помех в канале существуют различные по своей структуре и избыточности коды. Обычно избыточность кодов находится в пределах 10…60% или чуть больше. Избыточность 1/4 (25%) применяется при записи информации на лазерные диски и в системах цифрового спутникового ТВ.

Классификация кодов.

Известно большое число помехоустойчивых кодов, которые классифицируются по различным признакам. По­мехоустойчивые коды можно разделить на два больших класса: блочные и непрерывные. При блочном кодировании последова­тельность элементарных сообщений источника разбивается на от­резки и каждому отрезку ставится в соответствие определенная последовательность (блок) кодовых символов, называемая обыч­но кодовой комбинацией. Множество всех кодовых комбинаций, возможных при данном способе блочного кодирования, и есть блочный код.

Длина блока может быть как постоянной, так и переменной. Различают равномерные и неравномерные блоч­ные коды. Помехоустойчивые коды являются, как правило, рав­номерными.

Блочные коды бывают разделимыми и неразделимыми. К разделимым относятся коды, в которых символы по их назначению могут быть разделены на информационные символы, несущие ин­формацию о сообщениях и проверочные. Такие коды обознача­ются как (n , k ), где n - длина кода, k - число информационных символов. Число комбинаций в коде не превышает 2^ k . К нераздели­мым относятся коды, символы которых нельзя разделить по их назначению на информационные и проверочные.

Коды с постоянным весом характеризуются тем, что их кодо­вые комбинации содержат одинаковое число единиц: Примером такого кода является код “3 из 7”, в котором каждая кодовая комбинация содержит три единицы и четыре нуля (стандартных телеграфный код № 3).

???? ? ?????????? ????? ????????? ?????????? ??? ?????? ????????? q =1,..., n ?? ??????????? ???????, ????? ????? ???????, ?????????? ? ????, ????? ????? ?????, ?????????? ? ????????. ? ????????? ????????????? ???????, ? ???????? ????? ????? ?????? ???? ??? ?????? (?????????????? ?????? ? ??????? ??? ?????? ? ????), ????? ??? ????????? ??????????? ??? ??????. ? ???????????? ??????? ??????????? ??????????????? ?????? ????? ?????????? ??? ??????????? ?????????????? ????????? ????? ??????? ? ?????? ????:

где P ош вероятность искажения символа.

Среди разделимых кодов различают линейные и нелинейные. К линейным относятся коды, в которых поразрядная сумма по модулю 2 любых двух кодовых слов также является кодовым словом. Линейный код называется систематическим, если первые k символов его любой кодовой комбинации являются информаци­онными, остальные (n - k ) символов — проверочными.

????? ???????? ??????????????? ????? ???????? ??????? ??? (n , n - k ), ?????????? ???? ??????????? ??????, ???????? ????? ????? ?? ?????? 2 ???? ?????????????? ????????. ???? ???, ?????????? ????? ? ????????? ?? ????????, ????????? ?????????? ??? ????????? ?????? ???????? ?????????. ??????????? ?????????????? ?????? ? ?????? ??????????? ????? ?????????? ??? ??????????? ????????? ???? ????????:

Подклассом линейных кодов являются циклические коды. Они характеризуются тем, что все наборы, образованные циклической перестановкой любой кодовой комбинации, являются также кодо­выми комбинациями. Это свойство позволяет в значительной сте­пени упростить кодирующее и декодирующее устройства, особен­но при обнаружении ошибок и исправлении одиночной ошибки. Примерами циклических кодов являются коды Хэмминга, коды Боуза - Чоудхури - Хоквингема (БЧХ — коды) и др.

Примером нелинейного кода является код Бергера, у которо­го проверочные символы представляют двоичную запись числа единиц в последовательности информационных символов. Напри­мер, таким является код: 00000; 00101; 01001; O111O; 10001; 10110; 11010; 11111. Коды Бергера применяются в асиммет­ричных каналах. В симметричных каналах они обнаруживают все одиночные ошибки и некоторую часть многократных.

Непрерывные коды характеризуются тем, что операции коди­рования и декодирования производятся над непрерывной последо­вательностью символов без разбиения ее на блоки. Среди непре­рывных наиболее применимы сверточные коды.

Как известно различают каналы с независимыми и группирующимися ошибками. Соответственно помехоустойчивые коды можно разбить на два класса: исправляющие независимые ошибки и исправляющие пакеты ошибок. Далее будут рассматриваться в основном коды, исправляющие независимые ошибки. Это объясняется тем, что хотя для исправления пакетов ошибок раз­работано много эффективных кодов, на практике целесообразнее использовать коды, исправляющие независимые ошибки вместе с устройством перемежения символов или декорреляции ошибок. При этом символы кодовой комбинации не передаются друг за другом, перемешиваются с символами других кодовых комбинаций. Ес­ли интервал между символами, принадлежащими одной кодовой комбинации, сделать больше чем “память” канала, то ошибки в пределах кодовой комбинации можно считать независимыми, что и позволяет использовать коды, исправляющие независимые ошибки.

Блочные коды. Построение кодеков.

Линейные коды.

Из определения следует, что любой линейный код (п, k ) мож­но получить из k линейно независимых кодовых комбинаций пу­тем их посимвольного суммирования по модулю 2 в различных сочетаниях. Исходные линейно независимые кодовые комбина­ции называются базисными.

Представим базисные кодовые комбинации в виде матрицы размерностью n Xk

(7.7)

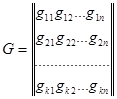В теории кодирования она называется порождающей. Тогда про­цесс кодирования заключается в выполнении операции: B = AG ,

где А- вектор размерностью k, соответствующий сообщению, В- вектор размерностью п, соответствующий кодовой комби­нации.

????? ???????, ??????????? ??????? (7.7) ???????? ??? ???????????? ??? ??????????? ??????????. ??? ?????? ?????????? ? ?????? ??????????? ??????????. ??? ????????? ???? ????? ?????? ????? k Xn ???????? ????????. ??? ????????? ??????? ???? ?????????? ?????????? ?????? ??????????

двоичных символов.

Две порождающие матрицы, которые отличаются друг от дру­га только порядком расположения столбцов, задают коды, ко­торые имеют одинаковые расстояния Хэмминга между соответствующими кодовыми комбинациями, а следовательно, одинако­вые корректирующие способности. Такие коды называются экви­валентными.

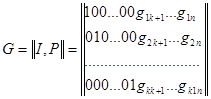? ???????? ???????? ?????????? ????? ???????? ??????? ??????????, ?????????? ?? ????? ??????? ????? ?????????????? ????????. ??? ???? ??????????? ??????? ??????? ???????? ? ???????????? ????? (7.8)

где I - единичная k Xk подматрица, P -k X( n - k )- подматрица проверочных символов, определяющая свойства кода. Матрица задает систематический код. Можно показать, что для лю­бого линейного кода существует эквивалентный систематический код.

???????? (п, k) ??? ????? ???? ????? ???????????? ???????? ? ??????????? ( r ?п). ??? ???? ?????????? В ??????????? ???? ?????? ? ??? ??????, ???? ?????? ? ???????????? ???? ??????? ??????? ?, ?. ?. ???? ??????????? ????????? (7.9)
??? ???????? ???????????????? ???????. ??? ??? ??? ????????? ??????????? ??? ????? ??????? ??????????, ??
???????????? ????? ??????? ? ????? ??? (7.10)

где P - подматрица, столбцами которой служат строки подмат­рицы Р (7.8), I-единичная r Xr подматрица. Подставляя (7.10) в (7.9), можно получать п—k уравнений вида (7.11)

??????? ?????????? ??????????? ????????. ?? (7.11) ???????, ??? ??????????? ??????? ??????? ?????????? ????????? ???? ?????????? ?????????? ????????? ???????????? ??????????????? ????????. ??????? ? ????? j -? ?????? ?????????? ?, ???????? ? ??????????? ??????? (7.10), ?????????, ????? ?????????????? ??????? ????????? ? ???????????? j -?? ????????????? ???????.

Очевидно, что линейный (п, k) код можно построить, исполь­зуя уравнения проверки (7.11). При этом первые k символов ко­довой комбинации информационные, а остальные п-k симво­лов - проверочные, образуемые в соответствии с (7.11).

--> ЧИТАТЬ ПОЛНОСТЬЮ <--