Реферат: Измерение геометрических величин в курсе средней школы

Задача 2.

Докажите, что стороны треугольника обратно пропорциональны его высотам, то есть:

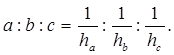
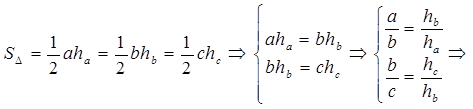
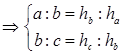. Так как 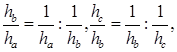получаем:

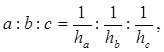что требовалось доказать.

Задача 3.

Докажите, что среди всех параллелограммов с данными диагоналями наибольшую площадь имеет ромб.

M B C

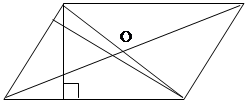
A K D

1-ый способ .

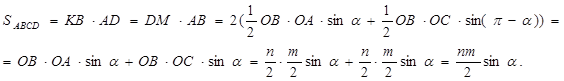
Если - ромб, то , то есть 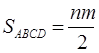. Наибольшее значение произведения зависит от наибольшего значения , которое достигается при , если , то . Следовательно, площадь ромба наибольшая среди всех площадей параллелограммов с данными диагоналями.

2-ой способ .

Составим функцию, выражающую площадь параллелограмма:

при .

Так как - наименьший угол, образуемый диагоналями при пересечении, то и будет точкой максимума, следовательно: ; и этот параллелограмм – ромб.

Задача 4.

Прямая, перпендикулярная высоте треугольника, делит его площадь пополам. Найдите расстояние от этой прямой до вершины треугольника, из которой проведена высота, если она равна .

B

A D C

- трапеция, то есть подобен

Так как для подобных треугольников их площади относятся как квадраты соответствующих линейных размеров, то: