Реферат: Измерение параметров АЦП

Дифференциальная нелинейность δ_н.д определяется отклонением приращения выходного сигнала преобразо­вателя от номинального значения младшего разряда при последовательном изменении кодового входного сигнала на единицу. Дифференциальная нелинейность идеально­го преобразователя равна нулю. Это означает, что при изменении входного кода преобразователя на единицу его выходной сигнал изменяется на значение младшего разряда. Допустимым значением дифференциальной не­линейности считается (1/2 )[ПВ1] Δ(1/2 значения младшего раз­ряда).

Дифференциальная нелинейность может быть вычис­лена таким образом. Для конкретного m-разрядного пре­образователя расчетное значение единицы младшего раз­ряда Δ_р =[U_п.ш /(2^m —l).

обеспечивающее контроль схем различного назначения, обычно сложное и дорогостоящее. Установки специаль­ного назначения, контролирующие схемы, как правило, одного типа, выполняют контроль быстрее, и с ними мо­гут работать люди, не обладающие большим опытом и мастерством.

В преобразователях с высокой разрешающей способ­ностью необходимо проконтролировать большое количе­ство параметров для получения информации о работе преобразователя. Например, 12-разрядный ЦАП или АЦП имеет 2¹² , или 4096, возможных комбинаций вход— выход. Безусловно, без применения автоматизированной высокопроизводительной установки решить проблему контроля подобных преобразователей невозможно.

При контроле ИМС АЦП, особенно многораз­рядных, необходимо соблюдать меры предосторожности при подключении контролируемого преобразователя к установке контроля. Линии связи должны быть такой длины и такого сопротивления, чтобы падение напряже­ния на них не вызвало значительного увеличения по­грешности измерения параметров ИМС АЦП.

Если проверяют ЦАП с токовым выходом, то к его выходу подключают операционный усилитель, обеспечи­вающий преобразование выходного тока ЦАП в напря­жение. При этом резистор обратной связи, входящий в состав ЦАП, подключают без подстроечных потенцио­метров, чтобы можно было измерить погрешность сме­щения нуля и полной шкалы.

Далее перед измерением параметров ЦАП нужно определенное время для его прогрева, чтобы обеспечить установившийся тепловой режим контроля. Это относит­ся в первую очередь к контролю нелинейности ЦАП, поскольку требуется большое количество измерений, за время которых из-за нагрева ЦАП его параметры могут существенно измениться. Например, у ЦАП с рассеивае­мой мощностью порядка 500 мВт время прогрева в зави­симости от типа корпуса колеблется от 5 до 15 мин.

С целью уменьшения времени контроля желательно проводить контроль параметров ЦАП не во всех точках его выходной характеристики. Минимальный объем по­лучаем при контроле значений всех разрядов, включае­мых по одному. Однако такой контроль допустим только в случае малого взаимного влияния разрядов, когда все разряды или комбинации разрядов, которые включаются, полностью независимы от включенного (выключенного) состояния других разрядов. В противном случае для по­лучения достоверного результата следует производить контроль по всем дискретным значениям выходного сиг­нала, т. е. в 2^m очках характеристики.

Далее будут рассмотрены методы контроля статичес­ких и динамических параметров ИМС АЦП, ко­торые могут быть использованы в автоматизированных системах контроля, предназначенных как для обеспече­ния серийного производства ИМС АЦП, так и для их входного контроля.

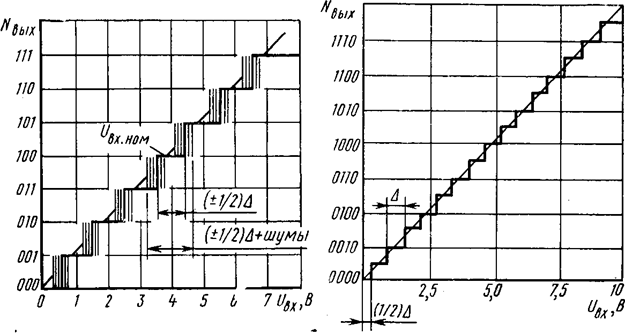
Рис. 4. Характеристика АЦП при наличии шума Рис. 5. Характеристика идеального четырехразрядного АЦП

3. Контроль статических параметров ИМС АЦП

Из-за неопределенности квантования при аналого-цифровом преобразовании, равной 1/2 значения младшего раз­ряда Δ, контроль АЦП представляет большие трудности по сравнению с контролем ЦАП, поскольку приходится не просто измерять выходной сигнал для заранее определённого кода (в случае ЦАП), но также определять как выходной код, так и точку (момент) изменения выходного кода при непрерывном изменении входного напряжения. Шумы (в преобразуемом сигнале или в преобразователе) вносят неопределенность в точное задание аналоговых входных величин, при которых происходят кодовые преобразования выходных сигналов, а также увеличивают диапазон квантования. Характер погрешности, обуслов­ленной влиянием шума, показан на рис. 4.

При отсутствии шума и погрешности линейности АЦП изменение выходного кода происходит при номинальных значениях входного напряжения. При отсутствии шума и наличии допустимых погрешностей линейности АЦП выходной код изменяется при изменении входного напряжения относительно его номинального значения на (±1/2) Δ. Шумы вызывают увеличение неопределенности момента изменения выходного кода (шумы показаны на рис. 4 в виде тонких линий).

Отметим, что точность АЦП не может быть лучше его разрешающей способности. В ЦАП, напротив, техниче­ские требования по точности превосходят требования по разрешающей способности. Такое различие объясняется противоположным характером этих преобразователей:

выход ЦАП может с высокой точностью воспроизводить уровень, являющийся мерой точного числа, между тем как выходной уровень АЦП определяется любой вход­ной величиной в пределах кванта.

Наибольшим числом контролируемых параметров об­ладают АЦП последовательного приближения, в котором применяются ЦАП и компаратор в цепи обратной связи. Эти преобразователи, так же как и ЦАП, характеризуют­ся дифференциальной нелинейностью и немонотонностью в отличие от интегрирующих АЦП, у которых может на­блюдаться только нелинейность. На рис. 5 показана выходная характеристика идеального четырехразрядного АЦП, каждая ступенька которой постоянна по ширине и равна Δ. Тем не менее даже для идеального АЦП (всех типов) существует неопределенность, равная (±1/2)А относительно входного напряжения, соответствующего какому-либо выходному коду АЦП. У реального АЦП (имеющего нелинейность) неопределенность возрастает до суммы погрешностей квантования и линейности. Если ЦАП, применяемый в АЦП последовательного приближения, нелинеен, то размер ступеньки отклонится от идеального значения и напряжения переходов сдвинутся от напряжении идеальных переходов. На рис. 10.30 при­ведена характеристика АЦП, внутренний ЦАП которого имеет погрешности разрядов: δ₁ =(l/2)A (при коде 1000), δ₂ =(—1/2)А (при коде 0100), δ₃ =0 (при коде 0010), δ₄ =0 (при коде 0001). Области рис. 10.30, отме­ченные пунктирными кружками, свидетельствуют о том, что изменения в по­грешности дифференци­альной линейности (а следовательно, и в по­грешности линейности) имеют место при пере­носах кода.Метод контроля па­раметров АЦП, кото­рый необходимо ис­пользовать в каждом конкретном случае, за­висит от многих причин. Одна из них—время преобразования контро­лируемого АЦП. Для преобразователей со временем преобразова­ния менее 100 мкс (пре­образователи последовательного .приближения) могут быть использованы все методы контроля. Иначе обстоит дело при контроле «медленных» АЦП. Например, пре­образователи интегрирующего типа, время преобразова­ния которых составляет десятки и сотни миллисекунд, не могут быть исследованы динамическим методом, преду­сматривающим наблюдения погрешности с помощью ос­циллографа.Простейший метод контроля параметров АЦП за­ключается в применении образцового ЦАП для форми­рования входного аналоговового сигнала контролируемо­го АЦП и в последующем сравнении входного кода об­разцового ЦАП и выходного кода АЦП. Однако он не определяет точного значения входного сигнала в момент перехода кода в пределах А. Поэтому таким методом можно определить точность калибровки (погрешность шкалы), нелинейность, дифференциальную нелинейность АЦП с погрешностью контроля не менее Δ. Рассмотрим схемы нескольких устройств, позволяющих автоматизировать процесс контроля параметров АЦП, в которых ис­пользуется многоразрядный образцовый ЦАП, предна­значенный для формирования входного сигнала АЦП ли­бо для восстановления аналогового сигнала из выходно­го кода АЦП. При этом линейность ЦАП должна быть на порядок выше линейности проверяемого АЦП.

На рис. 6 представлена схема одного из таких устройств. С генератора Г напряжение синусоидальной формы U_вх поступает на вход контролируемого АЦП и

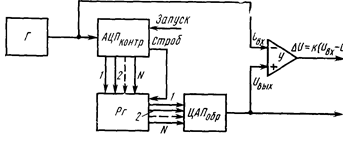
Рис. 6. Схема устройства автоматического контроля парамет­ров АЦП

на один из входов дифференциального усилителя У. Ре­зультат преобразования в виде кода N_i с частотой запус­ка АЦП заносится в регистр. Затем код N_i преобразует­ся с помощью образцового ЦАП (разрядность которого должна быть, по крайней мере, на четыре единицы боль­ше разрядности контролируемого АЦП) в аналоговый сигнал U_выx , подаваемый на другой вход усилителя. Раз­ностный сигнал усилителя ΔU=k( U_вх — U_выч ) характе­ризуется суммой погрешности квантования (±1/2)А и погрешности линейности АЦП. Следует учитывать, что любой сдвиг по фазе между входным сигналом АЦП и задержанным выходным сигналом ЦАП дает дополни­тельную погрешность. Поэтому для минимизации этой дополнительной погрешности частота входного сигнала должна быть достаточно низкой и определять ее необхо­димо исходя из быстродействия контролируемого АЦП и образцового ЦАП.

На рис. 7 приведена схема еще одного устройства автоматического контроля АЦП, где образцовый ЦАП используется в качестве формирователя входного воздей­ствия на контролируемый преобразователь. Формирователь кодов ФК обеспечивает формирование на цифровых входах образцового ЦАП любой требуемой кодовой ком­бинации. Выходное напряжение ЦАП подается на вход контролируемого АЦП. Цифровой код Ni с АЦП переда­ется в запоминающий регистр ЗРг после каждого преоб­разования. Цифровое слово Ni’, присутствующее на входе образцового ЦАП, вычитается в устройстве ВУ из кода Ni и цифровая ошибка ΔN=Ni—Ni’ подается на ЦАП с низкой разрешающей способностью, на выходе которого

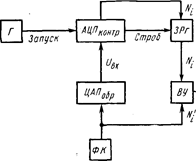
Рис. 7. Схема устройства контроля АЦП с разбраковкой резуль­тата контроля

она представляется в аналоговой форме. Кроме того, цифровая ошибка ΔN может быть подана на цифровой компаратор ЦК, в который занесены верхний и нижний пределы ее допустимых значений, что позволяет произве­сти проверку АЦП по принципу «годен—не годен», т. е. разбраковку контролируемых преобразователей. Разре­шающая способность образцового ЦАП в данной схеме, как и в предыдущей, должна быть на порядок выше, чем в контролируемом АЦП, чтобы уровень квантования ана­логового сигнала на входе АЦП не ограничивал разре­шающую способность считывания ошибки.

Как указывалось, сложность контроля параметров АЦП заключается в том, что каждому его выходному числовому коду соответствует определенная непрерывная аналоговая входная величина (ширина ступеньки на рис. 5, 10.30), крайние значения которой формируют со­ответствующие смежные числовые переходы. Поэтому для более качественного контроля характеристик АЦП тре­буется определение значения каждого из переходных уровней входного напряжения, что не обеспечивается пре­дыдущей схемой.

На рис. 8 изображена схема устройства, осущест­вляющего контроль выходной характеристики АЦП с ав­томатическим поиском переходных уровней. Это достига­ется включением контролируемого АЦП в цепь обратной связи, регулирующей его входное напряжение. Цифровой код Ni определяемого перехода с формирователя кодов ФК поступает на цифровой компаратор ЦК и на образ

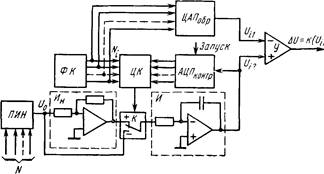
Рис. 8. Схема устройства контроля АЦП с автоматическим поиском переходных уровней

цовый ЦАП. На другой вход компаратора подается вы­ходной цифровой сигнал контролируемого АЦП. Цифро­вой компаратор вырабатывает сигнал, управляющий ключом К, через который на вход интегратора И посту­пает напряжение Но определенной полярности, формируе­мое программируемым источником напряжения ПИН и инвертором Ин. Система сфазирована таким образом, что изменяющееся выходное напряжение интегратора прибли­жает выходной код АЦП к записанному в компаратор коду Ni. В момент достижения равенства кодов направ­ление изменения выходного напряжения интегратора из­меняется на противоположное вследствие переключения ключа К. В дальнейшем процесс продолжается при пе­риодическом пилообразном колебании выходного напря­жения интегратора вблизи уровня перехода. Точность, с которой производится поиск уровня перехода, определя­ется постоянной времени Т интегратора, его входным ин­тегрируемым напряжением Uo и быстродействием конт­ролируемого АЦП. Действительно, приращение ΔU_и выходного напряжения интегратора за время интегрирова­ния t_и определяется соотношением

ΔU_и =U₀