Реферат: Изучение технологии нейронных сетей в профильном курсе информатики

блок, обозначенный F, принимает сигнал NET и выдает сигнал OUT. Если блок F сужает диапазон изменения величины NET так, что при любых значениях NET значения OUT принадлежат некоторому конечному интервалу, то F называется сжимающей функцией. В качестве сжимающей функции часто используется логистическая или сигмоидальная (S-образная) функция, показанная на рис.3. Эта функция математически выражется как F(x)=1/(1+e^-x ) . Таким образом,

OUT=1/(1+e^-NET )

По аналогии с электронными системами активационную

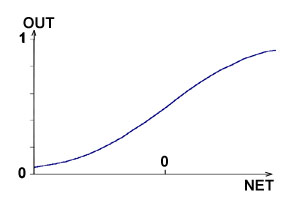рис.3.Сигмоидальная логистическая функция

функцию можно считать нелинейной усилительной характеристикой искусственного нейрона. Коэффициент усиления вычисляется как отношение приращения величины OUT к вызвавшему его небольшому приращению величины NET. Он выражается наклоном кривой при определенном уровне возбуждения и изменяется от малых значений при больших отрицательных возбуждениях (кривая почти горизонтальна) до максимального значения при нулевом возбуждении и снова уменьшается, когда возбуждение становится большим положительным. Гроссберг (1973) обнаружил, что подобная нелинейная характеристика решает поставленную им дилемму шумового насыщения. Каким образом одна и та же сеть может обрабатывать как слабые, так и сильные сигналы? Слабые сигналы нуждаются в большом сетевом усилении, чтобы дать пригодный к использованию выходной сигнал. Однако усилительные каскады с большими коэффициентами усиления могут привести к насыщению выхода шумами усилителей (случайными флуктуациями), которые присутствуют в любой физически реализованной сети. Сильные входные сигналы в свою очередь также будут приводить к насыщению усилительных каскадов, исключая возможность полезного использования выхода. Центральная область логистической функции, имеющая большой коэффициент усиления, решает проблему обработки слабых сигналов, в то время как в области с падающим усилением на положительном и отрицательном концах подходят для больших возбуждений. Таким образом, нейрон функционирует с большим усилением в широком диапазоне уровня входного сигнала.

Рассмотренная простая модель искусственного нейрона игнорирует многие свойства своего биологического двойника. Например, она не принимает во внимание задержки во времени, которые воздействуют на динамику системы. Входные сигналы сразу же порождают выходной сигнал. И что более важно, она не учитывает воздействий функции частотной модуляции или синхронизирующей функции биологического нейрона, которые ряд исследователей считают решающими. Несмотря на эти ограничения, сети, построенные из этих нейронов, обнаруживают свойства, сильно напоминающие биологическую систему. Только время и исследования смогут ответить на вопрос, являются ли подобные совпадения случайными или следствием того, что в модели верно схвачены важнейшие черты биологического нейрона.

Однослойные искусственные нейронные сети

Хотя один нейрон и способен выполнять простейшие процедуры распознавания, сила нейронных вычислений проистекает от соединений нейронов в сетях. Простейшая сеть состоит из группы нейронов, образующих слой, как показано в правой части рис.4.

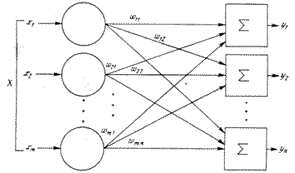рис.4.Однослойная нейронная сеть

Отметим, что вершины круги слева служат лишь для распределения входных сигналов. Они не выполняют каких-либо вычислений, и по этой причине они обозначены кругами чтобы отличать их от вычисляющих нейронов обозначенных квадратами Каждый элемент из множества входов X отдельным весом соединен с каждым искусственным нейроном. А каждый нейрон выдает взвешенную сумму входов в сеть. В искусственных и биологических сетях многие соединения могут отсутствовать, все соединения показаны в целях общности. Могут иметь место также соединения между выходами и входами элементов в слое.

Удобно считать веса элементами матрицы W. Матрица имеет m строк n столбцов, где m-число входов, а n-число нейронов. Например, w_3,2 -это вес, связывающий третий вход со вторым нейроном, таким образом вычисление выходного выходного вектора N, компонентами которого являются выходы OUT нейронов, сводится к матричному умножению N=XW, где N и X -векторы строки.

Многослойные искусственные нейронные сети

Более крупные и сложные нейронные сети обладают, как правило, и большими вычислительными способностями. Хотя созданы сети всех конфигураций, какие только можно себе представить, послойная организация нейронов копирует слоистые структуры определенных отделов головного мозга. Оказалось, что такие многослойные сети обладают большими возможностями, чем однослойные и в последние годы были разработаны алгоритмы для их обучения. Многослойные сети могут образовываться каскадами слоев. Выход одного слоя является входом для последующего слоя. Подобная сеть показана на рис.5 и снова изображена со всеми соединениями.

Нелинейная активационная функция

Многослойные сети могут привести к увеличению вычислительной мощности по сравнению с однослойной лишь в том случае, если активационная функция между слоями будет нелинейной.

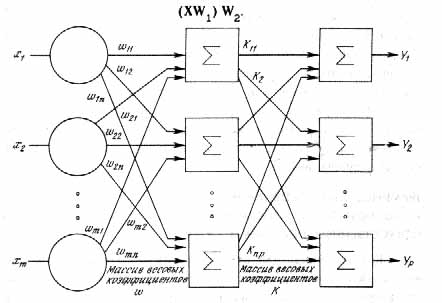Рис.5.Двуслойная нейронная сеть

Вычисление выхода слоя заключается в умножении входного вектора на первую весовую матрицу с последующим умножением (если отсутствует нелинейная активационная функция) результирующего вектора на вторую весовую матрицу. Это показывает, что двухслойная линейная сеть эквивалентна одному слою с весовой матрицей, равной произведению двух весовых матриц. Таким образом, для расширения возможностей сетей по сравнению с однослойной сетью необходима нелинейная однослойная функция.

Сети с обратными связями

У сетей, рассмотренных до сих по, не было обратных связей, т.е. соединений, идущих от выходов некоторого слоя к входам этого же слоя или предшествующих слоев. Этот специальный класс сетей называемых сетями прямого распространения представляет интерес и широко используется. Сети более общего вида имеющие соединения от выходов ко входам, называются сетями с обратными связями. У сетей без обратных связей нет памяти: их выход полностью определяется текущими входами и значениями весов. В некоторых конфигурациях сетей с обратными связями предыдущие значения выходов возвращаются на входы; выход, следовательно, определяется как текущим входом, так и предыдущими выходами. По этой причине сети с обратными связями могут обладать свойствами сходными с кратковременной человеческой памятью, сетевые выходы частично зависят от предыдущих входов.

Терминология

К сожалению, для искусственных нейронных сетей еще нет опубликованных стандартов и устоявшихся терминов, обозначений и графических представлений. Порой идентичные сетевые парадигмы, представленные различными авторами, покажутся далекими друг от друга. В этой книге выбраны наиболее широко используемые термины. Многие авторы избегают термина «нейрон» для обозначения искусственного нейрона, считая его слишком грубой моделью своего биологического прототипа. Здесь термины «нейрон», «клетка», «элемент» используются взаимозаменяемо для обозначения «искусственного нейрона» как краткие и саморазъясняющие.

Дифференциальные уравнения или разностные уравнения

Алгоритмы обучения, как и вообще искусственные нейронные сети, могут быть представлены как в дифференциальной, так и в конечноразностной форме. При использовании дифференциальных уравнений предполагают, что процессы непрерывны и осуществляются подобно большой аналоговой сети. Для биологической системы, рассматриваемой на микроскопическом уровне, это не так. Активационный уровень биологического нейрона определяется средней скоростью, с которой он посылает дискретные потенциальные импульсы по своему аксону. Средняя скорость обычно рассматривается как аналоговая величина, но важно не забывать о действительном положении вещей. Если моделировать искусственную нейронную сеть на аналоговом компьютере, то весьма желательно использовать представление с помощью дифференциальных уравнений. Однако сегодня большинство работ выполняется на цифровых компьютерах, что заставляет отдавать предпочтение конечно-разностной форме как наиболее легко программируемой. По этой причине на протяжении всей книги используется конечно-разностное представление.

Графическое представление

Как видно из публикаций, нет общепринятого способа подсчета числа слоев в сети. Многослойная сеть состоит из чередующихся множеств нейронов и весов. Ранее в связи с рис.1.5 уже говорилось, что входной слой не выполняет суммирования. Эти нейроны служат лишь в качестве разветвлений для первого множества весов и не влияют на вычислительные возможности сети. По этой причине первый слой не принимается во внимание при подсчете слоев, и сеть, подобная изображенной на рис. 1.5, считается двухслойной, так как только два слоя выполняют вычисления. Далее, веса слоя считаются связанными со следующими за ними нейронами. Следовательно, слой состоит из множества весов со следующими за ними нейронами, суммирующими взвешенные сигналы.

Обучение искусственных нейронных сетей

Среди всех интересных свойств искусственных нейронных сетей ни одно не захватывает так воображения, как их способность к обучению. Их обучение до такой степени напоминает процесс интеллектуального развития человеческой личности, что может показаться, что достигнуто глубокое понимание этого процесса. Но, проявляя осторожность, следует сдерживать эйфорию. Возможности обучения искусственных нейронных сетей ограничены, и нужно решить много сложных задач, чтобы определить, на правильном ли пути мы находимся. Тем не менее, уже получены убедительные достижения, такие как «говорящая сеть» Сейновского, и возникает много других практических применений.

Цель обучения

Сеть обучается, чтобы для некоторого множества входов давать желаемое (или, по крайней мере, сообразное с ним) множество выходов. Каждое такое входное (или выходное) множество рассматривается как вектор. Обучение осуществляется путем последовательного предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной процедурой. В процессе обучения веса сети постепенно становятся такими, чтобы каждый входной вектор вырабатывал выходной вектор.

Обучение с учителем

Различают алгоритмы обучения с учителем и без учителя. Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе они называются обучающей парой. Обычно сеть обучается на некотором числе таких обучающих пар. Предъявляется выходной вектор, вычисляется выход сети и сравнивается с соответствующим целевым вектором, разность (ошибка) с помощью обратной связи подается в сеть, и веса изменяются в соответствии с алгоритмом, стремящимся минимизировать ошибку. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.

Обучение без учителя

Несмотря на многочисленные прикладные достижения, обучение с учителем критиковалось за свою биологическую неправдоподобность. Трудно вообразить обучающий механизм в мозге, который бы сравнивал желаемые и действительные значения выходов, выполняя коррекцию с помощью обратной связи. Если допустить подобный механизм в мозге, то откуда тогда возникают желаемые выходы? Обучение без учителя является намного более правдоподобной моделью обучения в биологической системе. Развитая Кохоненом и многими другими, она не нуждается в целевом векторе для выходов и, следовательно, не требует сравнения с предопределенными идеальными ответами. Обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса сети так, чтобы получались согласованные выходные векторы, т.е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных векторов. Следовательно, выходы подобной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения. Это не является серьезной проблемой. Обычно не сложно идентифицировать связь между входом и выходом, установленную сетью.

Алгоритмы обучения.

Большинство современных алгоритмов обучения выросло из концепций Хэбба. Им предложена модель обучения без учителя, в которой синоптическая сила (вес) возрастает, если активированы оба нейрона, источник и приемник. Таким образом, часто используемые пути в сети усиливаются, и феномен привычки и обучения через повторение получает объяснение. В искусственной нейронной сети, использующей обучение по Хэббу, наращивание весов определяется произведением уровней возбуждения передающего и принимающего нейронов. Это можно записать как

w _ij (n + 1) = w_ij (n) + aOUT_i OUT_j

где w_ij (n)- значение веса от нейрона i к нейрону j до подстройки, w _ij (n + 1)- значение веса от нейрона i к нейрону j после подстройки, a- коэффициент скорости обучения, OUT_i - выход нейрона i и вход нейрона j, OUT_j - выход нейрона j.

Сети, использующие обучение по Хэббу, конструктивно развивались, однако за последние 20 лет были развиты более эффективные алгоритмы обучения. В частности, были развиты алгоритмы обучения с учителем, приводящие к сетям с более широким диапазоном характеристик обучающих входных образов и большими скоростями обучения, чем использующие простое обучение по Хэббу. В настоящее время используется огромное разнообразие обучающих алгоритмов. Потребовалась бы значительно большая по объему статья, чем эта, для рассмотрения этого предмета полностью. Чтобы рассмотреть этот предмет систематически, если и не исчерпывающе, в каждой из последующих глав подробно описаны алгоритмы обучения для рассматриваемой в главе парадигмы. В дополнение в приложении представлен общий обзор, в определенной мере более обширный, хотя и не очень глубокий. В нем дан исторический контекст алгоритмов обучения, их общая таксономия, ряд преимуществ и ограничений. В силу необходимости это приведет к повторению части материала, оправданием ему служит расширение взгляда на предмет. [6]

1.2 Влияние обучения технологии нейронных сетей на развитие мышления школьников

Установим связь между предметом изучаемой темы – искусственным интеллектом – и мышлением.

Как сложный познавательный процесс мышление издавна вызывает большой интерес у ученых. Возникло немало теорий, имеющих различные теоретические основания.

Рассмотрим наиболее известные теории, объясняющие процесс мышления [1]. Их можно разделить на две большие группы: те, которые исходят из гипотезы о наличии у человека природных, не изменяющихся под влиянием жизненного опыта интеллектуальных способностей, и те, в основу которых положено представление о том, что умственные способности человека в основном формируются и развиваются прижизненно.

Концепции, согласно которым интеллектуальные способности и сам интеллект определяются как совокупность внутренних структур, обеспечивающих восприятие и переработку информации с целью получения нового знания, составляют одну группу теорий мышления. Считается, что соответствующие интеллектуальные структуры существуют у человека с рождения в потенциально готовом виде, постепенно проявляясь (развиваясь) по мере взросления организма.

Эта идея априорно существующих интеллектуальных способностей – задатков – характерна для многих работ в теории мышления, выполненных в немецкой школе психологии. Наиболее отчетливо она представлена в гештальттеории мышления, согласно которой способность формировать и преобразовывать структуры, видеть их в реальной действительности и есть осно­ва интеллекта.

В современной психологии влияние идей обсуждаемых теорий прослеживается в понятии схемы. Давно замечено, что мыш­ление, если оно не связано с какой-либо конкретной, внешне детерминированной задачей, внутренне подчиняется определенной логике. Эту логику, которой следует мысль, не имеющая внешней опоры, называют схемой.