Реферат: Класифікація та основні властивості провідникових матеріалів

Рухаючись в металі, електрони мають корпускулярно – хвильову природу, а тому основними їх параметрами є не тільки маса (m), швидкість (v), енергія частки (W), але і частота та довжина хвилі:

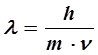
де h – постійна Планка, h = 6,62 · 10 ^{- 34} [Дж·с].

При звичайних температурах електрони в металах підпорядковуються статистиці Фермі – Дірака. Якщо в енергетичній зоні електронів менше ніж потрібно, щоб заповнити «заповнену зону», то вони займають рівні починаючи від «дна» зони знизу доверху.

Імовірність заповнення рівнів залежить від їх енергії і верхня межа заповнення стає розмитою. Криву розраховують за допомогою статистики Фермі:

якщо W = W_f то Р (W) = ,

де: W – енергія рівня, ймовірність заповнення якого визначається; W_f – енергія етапного рівня, на якому ймовірність заповнення дорівнює 0,5; k =1,38 • 10 ^–23 [Дж/K] – постійна Больцмана. Ця енергія відповідає верхній межі електронного розподілення при Р= 0, W_f – називають рівнем Фермі. Відповідний йому потенціал: називається електрохімічним потенціалом.

3. Властивості провідників

До найважливіших параметрів, які характеризують властивості провідникових матеріалів відносяться:

1. Питома провідність та питомий опір провідника. Зв’язок щільності струму J ([А/м² ]) та напруженості електричного поля Е ([В/м]) в провіднику пов’язані диференційною формою закону Ома:

де - це питома провідність провідника; величина ρ = 1/ – питомий опір провідника довжиною (l), з поперечним перерізом (S), у якого опір матеріалу (R).

.

Для вимірювання ρ провідникових матеріалів інколи користуються несистемною одиницею вимірювання або [мкОм·м]. Зв'язок між приведеними одиницями вимірювання має вигляд:

1 [Ом·м]=10⁶ [мкОм·м]=10⁶ [Ом·мм² /м]

Значення ρ для провідників з металу знаходяться в межах: 0,016 [мкОм·м] (для срібла)÷10 [мкОм·м] (для залізохромоалюмінієвих сплавів).

Питома провідність металевих провідників згідно з класичною теорією металів може бути визначена за формулою:

де е – заряд електрона; n₀ – число вільних електронів в одиниці об’єму; λ – середня довжина вільного пробігу електрона (відстань між вузлами решітки); μ – маса електрона; ν_т – середня швидкість теплового руху вільного електрона в металі.

При перетворенні останнього виразу на основі положень теорії квантової механіки, отримаємо:

де K – чисельний коефіцієнт.

Величини ν_т та n₀ для всіх металів приблизно однакові, тому значення питомої провідності γ головним чином визначається довжиною вільного пробігу електрону λ, яка в свою чергу визначається структурою матеріалу. Всі чисті метали з найбільш правильною кристалічною решіткою мають найменший питомий опір (ρ); при наявності домішок, кристалічна решітка пошкоджується, що приводить до зростання питомого опору (ρ).

До такого ж висновку можна прийти, на підставі хвилевої природи електронів. Розсіювання електронних хвиль відбувається на дефектах кристалічної решітки, які співрозмірні з відстанню, що становить близько чверті довжини електронної хвилі. Порушення менших розмірів не викликають помітного розсіювання хвиль. В металевих провідниках, де довжина хвилі електрона близько 0,5 [нм], мікродефекти створюють значну відстань, яка зменшує рухливість електронів, і відповідно, приводить до зростання питомого опору матеріалу(ρ).

Температурний коефіцієнт питомого опору металів

З ростом температури кількість вільних носіїв заряду в металевому провіднику залишається практично незмінною, але підсилюються коливання вузлів кристалічної решітки, що впливає на зменшення середньої довжини вільного пробігу електрону (λ) (кількість перешкод на шляху направленого вільного руху електронів зростає), як наслідок зменшується рухливість електронів, а це у свою чергу призводить до збільшення питомого опору металу (ρ).

ТКρ =

Таким чином ТКρ – температурний коефіцієнт питомого опору металів має позитивне значення.