Реферат: Классическая электродинамика
История развития классической электродинамики является поучительным примером того, как математизация естественно научной дисциплины и переход к изящному (хотя и достаточно сложному) языку описания повлекли за собой качественный скачок в понимании целого ряда явлений природы, часть из которых была первоначально предсказана теоретически (“на кончике пера”), а потом получила блестящее экспериментальное подтверждение. В настоящей теме будет содержаться достаточно большое количество математических формул, приводимых лишь с целью иллюстрации красоты и компактности языка математики.
Непрерывные распределения зарядов.
Входящие в выражения для электростатических и магнитостатических полей (9_4) и (9_8) суммы в случае макроскопических заряженных тел содержат очень большое число слагаемых, соответствующих вкладам в поля от точечных зарядов. Их вычисление неудобно с чисто “технической” точки зрения: математическая операция суммирования более трудоемка, чем, например, интегрирование (сказанное относится к аналитическим расчетам, при компьютерном счете суммирование предпочтительнее взятия интегралов, однако в 19 веке подобной альтернативы в математике не существовало). Переход к интегрированию требовал приближенной замены дискретного распределения элементарных зарядов на непрерывное, характеризуемое плотностью электрического заряда ![]() (отношение величины заряда к объему содержащего его небольшого, но макроскопического элемента пространства):
(отношение величины заряда к объему содержащего его небольшого, но макроскопического элемента пространства):
(1) ![]() .
.
Естественно, что замена (1) приводила к “сглаживанию” рассчитываемых макроскопических полей по сравнению с реальными микроскопическими, сильно изменяющимися на сравнимых с размером атома расстояниях. Описанный переход к непрерывному распределение зарядов существенно упрощал расчеты, не снижая их практическую ценность (наука и техника 19 века еще не доросли до эффектов, происходящих на микроскопическом уровне организации материи).
Математический формализм. Переход к непрерывным распределениям зарядов и токов позволил переписать законы электро и магнитостатики сразу в нескольких математических формах, эквивалентных по физическому смыслу, но существенно различающихся по технике выполнения конкретных расчетов:
интегральные формулировки:
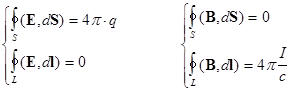 ;
;
дифференциальные формулировки:
(3) 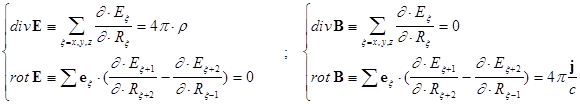 ;
;
расчет полей через скалярный ![]() и векторный
и векторный ![]() потенциалы:
потенциалы:
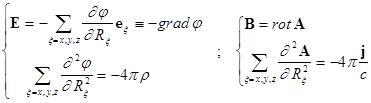 .
.
Т.о. адекватное описание одних и тех же законов естествознания возможно на различных языках математики.
Операторы.
В начале 20 века в математике были введены новые объекты - операторы, без использования которых современная физика была бы немыслима. Понятие оператора является естественным обобщением традиционного для классической математики понятия функции. Если под функцией понимается закон (правило, отображение), по которому одному числу (набору чисел) ставится в соответствие другое число (набор чисел), то под оператором подразумевают закон, по которому одному объекту (группе объектов) ставится в соответствие другой объект (группа). Наиболее часто встречаются операторы, действующие на функции (операторы умножения на число, дифференцирования, интегрирования и т.д.) или векторы (оператор поворота, проектирования и т.д.). Весьма полезной оказалась идея определения математических операций над операторами. Например, под произведением двух операторов подразумевается оператор, выполняющий последовательно действия каждого из перемножаемых операторов. Для операции умножения операторов в общем случае не выполняется свойство коммутативности:
(5) ![]() .
.
Использование языка операторов существенно сокращает запись многих математических формул и делает их более “элегантными”. Так введение лишь одного дифференциального оператора “набла”
![]()
при помощи стандартным образом определенных операций скалярного ( , ) и векторного [ , ] умножения позволяет записать системы уравнений (3) и (4) в весьма компактной форме:
(3’) 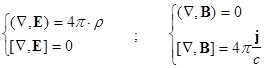 ;
;
(4’) ![]()
![]() ,
, 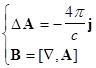 .
.
В последних равенствах использован оператор Лапласа:
(7) ![]() .
.
Помимо краткости записи преимущество операторного метода состоит в том, что. с самим оператором набла можно обращаться почти так же, как с обычным вектором, что, несомненно, облегчает громоздкие выкладки.
Закон электромагнитной индукции Фарадея.
Долгое время электрические и магнитные явления считались независимыми, хотя даже на уровне магнитостатики это не совсем верно: магнитостатическое поле порождается постоянными токами, существование которых в веществе невозможно без наличия электрического поля. Фарадей экспериментальным путем установил, что изменяющееся во времени магнитное поле может порождать электрическое. Это электрическое поле в отличие от порождаемого зарядами потенциального электростатического является вихревым, т.е. его линии представляют собой замкнутые кривые (рис. 11_1). Открытый Фарадеем закон индукции впоследствии имел колоссальное практическое значение, поскольку открыл весьма удобный и дешевый способ преобразования механической энергии движения источников магнитного поля в электрическую, ныне лежащий в основе промышленного производства электроэнергии.
С точки зрения математической записи уравнений для поля открытое Фарадеем явление требует видоизменения системы уравнений (6):
(10) 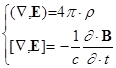 .
.
Гипотеза Максвелла. Рассмотрев совместно систему уравнений (7) и (10) Максвелл обратил внимание на следующие ее недостатки:
1. Указанная система несовместна с законом сохранения заряда.
2. Система оказалась весьма несимметричной даже для случая описания электромагнитного поля в пустом пространстве (![]() =0 и j=0).
=0 и j=0).
Несоответствие уравнений закону сохранения заряда было достаточным аргументом для того, чтобы усомниться в их истинности, поскольку законы сохранения носят весьма общий характер. Оказалось, что существует множество способов видоизменения системы уравнений (7), (10), приводящих их в соответствие с законом сохранения. Максвеллом был выбран простейший из возможных путь, приводящий систему к симметричному виду в случае ее использования для описания полей в пустом пространстве. В последнее уравнение было добавлено слагаемое, описывающее возможность генерации вихревого магнитного поля изменяющимся электрическим (“ток смещения”):
--> ЧИТАТЬ ПОЛНОСТЬЮ <--