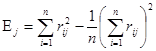Реферат: Кластерный анализ

Х15 - США

Х16 - Европе

Х17 - других странах

Запасы цинка у потребителей:

Х18 - в США

Х19 - в Англии

Х10 - в Японии

Импорт цинковых руд и концентратов (тыс. тонн)

Х21 - в США

Х22 - в Японии

Х23 - в ФРГ

Экспорт цинковых руд и концентратов (тыс. тонн)

Х24 - из Канады

Х25 - из Австралии

Импорт цинка (тыс. тонн)

Х26 - в США

Х27 - в Англию

Х28 - в ФРГ

Экспорт цинка (тыс. Тонн)

Х29 - из Канады

Х30 - из Австралии

Для определения конкретных зависимостей был использован аппарат корреляционно-регрессионного анализа. Анализ связей производился на основе матрицы парных коэффициентов корреляции. Здесь принималась гипотеза о нормальном распределении анализируемых показателей конъюнктуры. Ясно, что rij являются не единственно возможным показателем связи используемых показателей. Необходимость использования кластерного анализа связано в этой задаче с тем, что число показателей влияющих на цену цинка очень велико. Возникает необходимость их сократить по целому ряду следующих причин:

а) отсутствие полных статистических данных по всем переменным;

б) резкое усложнение вычислительных процедур при введении в модель большого числа переменных;

в) оптимальное использование методов регрессионного анализа требует превышения числа наблюдаемых значений над числом переменных не менее, чем в 6-8 раз;

г) стремление к использованию в модели статистически независимых переменных и пр.

Проводить такой анализ непосредственно на сравнительно громоздкой матрице коэффициентов корреляции весьма затруднительно. С помощью кластерного анализа всю совокупность конъюнктурных переменных можно разбить на группы таким образом, чтобы элементы каждого кластера сильно коррелировали между собой, а представители разных групп характеризовались слабой коррелированностью.

Для решения этой задачи был применен один из агломеративных иерархических алгоритмов кластерного анализа. На каждом шаге число кластеров уменьшается на один за счет оптимального, в определенном смысле, объединения двух групп. Критерием объединения является изменение соответствующей функции. В качестве функции такой были использованы значения сумм квадратов отклонений вычисляемые по следующим формулам: