Реферат: Кодирование
Чаще всего используется при передаче данных кода ASCII; каждый символ можно считать строкой массива. Такая проверка может не только установить факт ошибки, но и обнаружить ее место, а значит, есть принципиальная возможность ее исправления, хотя это практически не используется.
1 0 1 1 0 1 1 1
0 1 0 0 0 1 0 0
1 0 1 0 0 1 0 1
1 1 0 0 1 0 1 0
0 0 0 1 0 1 0 0
1 0 0 0 1 0 0
После обнаружения ошибок иногда можно повторить передачу сообщений, иногда после обнаружения ошибки предпринимается вторая и даже третья попытка передачи сообщения.
Проверка на четность широко используется на ЭВМ, как на аппаратном, так и на программном уровне.
Например, при считывании с магнитной ленты в случае, когда условие на четность не выполняется, то производится повторное считывание, т. е. если произошла малая потеря намагниченности, то после второй попытки может быть считывание произойдет правильно.
Пример 1. Символы алфавита источника кодируются семиразрядным двоичным кодом с весом кодовых векторов (количеством единиц в кодовой комбинации) w = 3. Определить необходимую мощность кода и его избыточность.
Решение: Мощность семиразрядного кода равна N = 27 = 128.
Так как для кодирования используются только кодовые вектора с весом три , то количество таких векторов в семиразрядном коде равно
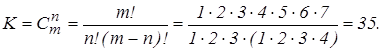
Избыточность кода равна R = 1 – log2 K/ log2 N = 0,265.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Семенюк В. В. Экономное кодирование дискретной информации. – СПб.: СПб ГИТМО (ТУ), 2001;
2. Мастрюков Д. Алгоритмы сжатия информации. Ч. 1. Сжатие по Хаффмену //Монитор, 1993. – № 7 – 8 – С. 14 – 20;
3. Мастрюков Д. Алгоритмы сжатия информации. Ч. 2. Арифметическое кодирование //Монитор, 1994 – № 1 – С. 20 – 23;
4. Ф.Дж.Мак-Вильямс, Н.Дж.А.Слоэн, Теория кодов, исправляющих ошибки, Москва, “Связь”, 1979.
5. .Лидл, Г.Нидеррайтер, Конечные поля, Т. 1,2, Москва, “Мир”, 1988.
6. Т.Касами, Н.Токура, Е.Ивадари, Я.Инагаки, Теория кодирования, Москва, “Мир”, 1978.
7. У.Петерсон, Э.Уэлдон, Коды, исправляющие ошибки, Москва, “Мир”, 1976.
8. Э.Берлекэмп, Алгебраическая теория кодирования, Москва, “Мир”, 1971.
9. Дискретная математика и математические вопросы кибернетики. Т.1. /Ю.Л. Васильев, Ф. Я. Ветухновский, В. В. Глаголев, Ю. И. Журавлев, В. И. Левенштейн, С. В. Яблонский. Под общей редакцией С. В. Яблонского и О. Б. Лупанова. – М.: Главная редакция физико – математической литературы изд–ва «Наука», 1974
10. Лидовский В. В. Теория информации: Учебное пособие. — М.: Компания Спутник+, 2004