Реферат: Кодовый замок
В теории автоматов проводится их классификация по ряду признаков. Не вдаваясь в подробности, отметим, что в схемотехнике преобладают автоматы Мура, выходы которых являются функциями только состояния автомата. Для этого автомата QH = f(Q, X) и Y = φ(Q).
Зависимость выходов и от состояния автомата и от вектора входных переменных свойственна автоматам Мили.
Некоторые функциональные узлы принадлежат к числу автономных автоматов, которые не имеют информационных входов, и под действием тактовых сигналов переходят из состояния в состояние по алгоритму, определяемому структурой автомата.
В нашем случае, для формирования последовательности выходных сигналов Y = {Z1 , Z2 } при соответствующей последовательности входных сигналов (A, B, C)i , можно использовать автомат с жесткой логикой и законом функционирования автомата Мили :
Qt+1 = f(Qt , ABCt );
Yt = φ(Qt , ABCt ),
где: Q = {Q1 , Q2 , Q3 , Qn } – множество состояний автомата; t = 0, 1, 2, 3, 4,…
I. Абстрактный синтез автомата.
 |
1.1)
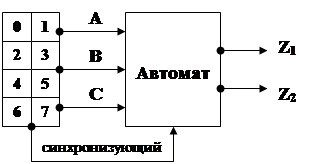
Интерфейс автомата (рис. 2).
Алфавит состояний автомата
| D4 | D3 | D2 | D1 | D0 | |
| Q0 | 0 | 0 | 0 | 0 | 0 |
| Q1 | 0 | 0 | 0 | 0 | 1 |
| Q2 | 0 | 0 | 0 | 1 | 0 |
| Q3 | 0 | 0 | 0 | 1 | 1 |
| Q4 | 0 | 0 | 1 | 0 | 0 |
| Q5 | 0 | 0 | 1 | 0 | 1 |
| Q6 | 0 | 0 | 1 | 1 | 0 |
| Q7 | 0 | 0 | 1 | 1 | 1 |
| Q8 | 0 | 1 | 0 | 0 | 0 |
| Q9 | 0 | 1 | 0 | 0 | 1 |
| Q10 | 0 | 1 | 0 | 1 | 0 |
| Q11 | 0 | 1 | 0 | 1 | 1 |
| Q12 | 0 | 1 | 1 | 0 | 0 |
| Q13 | 0 | 1 | 1 | 0 | 1 |
| Q14 | 0 | 1 | 1 | 1 | 0 |
| Q15 | 0 | 1 | 1 | 1 | 1 |
| Q16 | 1 | 0 | 0 | 0 | 0 |
В соответствии с заданием и алфавитом состояний строим граф переходов
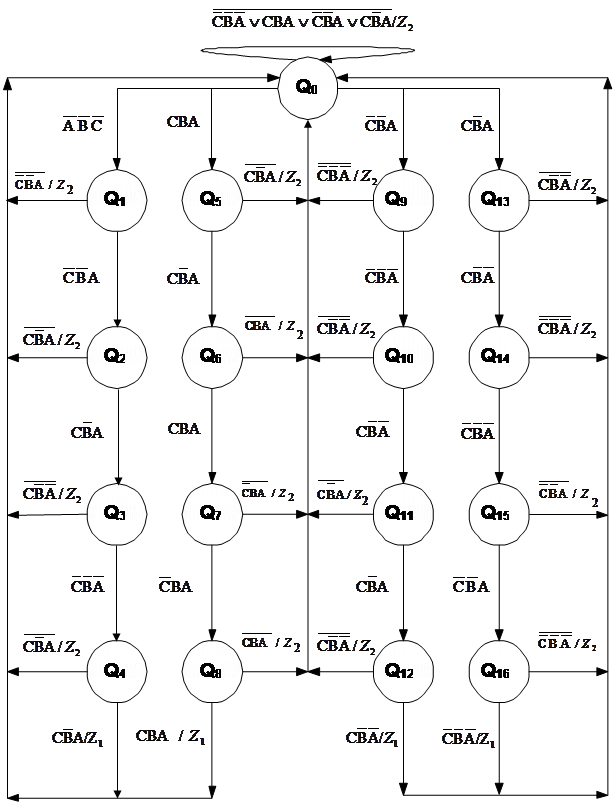 |
В соответствии с графом переходов и таблицей состояний строим таблицу переходов
| Q | C | B | A | (CBA) | Z1 | Z2 | Qн | ||||||||||
| D4 | D3 | D2 | D1 | D0 | D4 | D3 | D2 | D1 | D0 | ||||||||
| Q0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | Q1 |
| Q0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 7 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | Q5 |
| Q0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | Q9 |
| Q0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 5 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | Q13 |
| Q1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | Q2 |
| Q2 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | Q3 |
| Q3 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | Q4 |
| Q4 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | Q0 /Z1 |
| Q5 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 5 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | Q6 |
| Q6 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 7 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | Q7 |
| Q7 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | Q8 |
| Q8 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | Q0 /Z1 |
| Q9 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | Q10 |
| Q10 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 4 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | Q11 |
| Q11 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 5 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | Q12 |
| Q12 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | Q0 /Z1 |
| Q13 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 4 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | Q14 |
| Q14 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | Q15 |
| Q15 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | Q16 |
| Q16 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | Q0 /Z1 |
Чтобы не загромождать таблицу переходами в состояние Q0 /Z2 , условимся, что при всех остальных комбинациях Q и CBA, не описанных в таблице, переход будет осуществляться так:
| Q | C | B | A | (CBA) | Z1 | Z2 | Qн | ||||||||||
| D4 | D3 | D2 | D1 | D0 | D4 | D3 | D2 | D1 | D0 | ||||||||
| Qx | x | x | x | x | x | все другие комбинации | x | 0 | 1 | 0 | 0 | 0 | 0 | 0 | Q0 /Z2 | ||
Далее можно было бы выводить функции переходов, минимизировать, упрощать, опять минимизировать… Но есть способ лучше – прошить все эти функции “как есть” в ПЗУ, а в качестве элементов памяти использовать параллельный регистр с двухступенчатыми D-триггерами. При этом состояние Q и сигналы CBA будут являться адресом ПЗУ, а Z1 , Z2 и Qн – данными, которые необходимо записать по этому адресу. Во все же остальные адреса необходимо записать 01000000.
I. Структурный синтез автомата.
2.1) Использование всех наборов исключает присутствие ложных комбинаций в функциональной схеме.
2.2) Введение дополнительного синхронизирующего провода в интерфейс автомата (рис № 2) позволяет использовать тактируемый регистр с двухступенчатыми триггерами, которые, в свою очередь, предотвращают возможные гонки в автомате.
2.3) На странице № 7 реализуем функциональную схему.
Набор элементов для физического синтеза.
В качестве элементной базы можно использовать регистры с разрядностью ≥ 7 и асинхронным сбросом, ПЗУ с разрядностью адресов ≥ 8 и разрядностью данных ≥ 7, например, соответственно, 74LS199 и 573РФ2.
Остается добавить, что работоспособность автомата была проверена в системе проектирования электронных схем CircuitMakerPro 6.0
Литература.
Е.Угрюмов «Цифровая схемотехника», BHV 2000.
«12» апреля 2001г. _________________
Схема автомата

Цепочка R1 C1 обеспечивает сброс регистра и приведение автомата в исходное состояние при включении питания.