Задача состоит в нахождений числа ошибок u, их позиций и их значений при известных синдромах Sj.

Предположим, для начала, что u в точности равно t. Запишем (1) в виде системы нелинейных уравнений в явном виде:

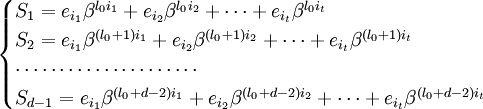
Обозначим через локатор k-ой ошибки, а через величину ошибки, . При этом все Xk различны, так как порядок элемента β равен n, и поэтому при известном Xk можно определить ik как ik = logβXk.

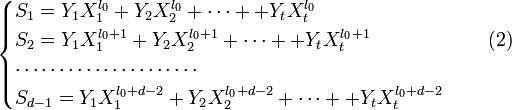
Составим полином локаторов ошибок:

Корнями этого полинома являются элементы, обратные локаторам ошибок. Помножим обе части этого полинома на . Полученное равенство будет справедливо для

:

Положим и подставим в (3). Получится равенство, справедливое для каждого и при всех :

Таким образом для каждого l можно записать свое равенство. Если их просуммировать по l, то получиться равенство, справедливое для каждого

:

.

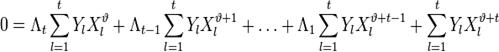Учитывая (2) и то, что

(то есть меняется в тех же пределах, что и ранее) получаем систему линейных уравнений:

.

Или в матричной форме

,

Где

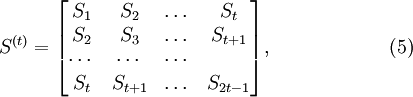
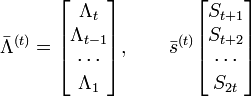
Если число ошибок и в самом деле равно t, то система (4) разрешима, и можно найти значения коэффициентов . Если же число u < t, то определитель матрицы S(t) системы (4) будет равен 0. Это есть признак того, что количество ошибок меньше t. Поэтому необходимо составить систему (4), предполагая число ошибок равным t − 1. Высчитать определитель новой матрицы S(t − 1) и т. д., до тех пор, пока не установим истинное число ошибок.

После этого можно решить систему (4) и получить коэффициенты полинома локаторов ошибок. Его корни (элементы, обратные локаторам ошибок) можно найти простым перебором по всем элементам поля GF(qm). К ним найти элементы, обратные по умножению, — это локаторы ошибок . По локаторам можно найти позиции ошибок (ik = logβXk), а значения Yk ошибок из системы (2), приняв t = u. Декодирование завершено.

Коды Рида–Соломона

Широко используемым подмножеством кодов БЧХ являются коды Рида-Соломона, которые позволяют исправлять пакеты ошибок. Пакет ошибок длины b представляет собой последовательность из таких b ошибочных символов, что первый и последний из них отличны от нуля. Существуют классы кодов Рида-Соломона, позволяющие исправлять многократные пакеты ошибок.

Коды Рида-Соломона широко используются в устройствах цифровой записи звука, в том числе на компакт-диски. Данные, состоящие из отсчетов объединяются в кадр, представляющий кодовое слово. Кадры разбиваются на блоки по 8 бит. Часть блоков являются контрольными.

Обычно 1 кадр (кодовое слово) = 32 символа данных +24 сигнальных символа +8 контрольных бит = 256 бит.

Сигнальные символы это вспомогательные данные, облегчающие декодирование: служебные сигналы, сигналы синхронизации и т. д.

При передаче данных производится перемежение (изменение порядка следования по длине носителя и во времени) блоков с различным сдвигом во времени, в результате чего расчленяются сдвоенные ошибки, что облегчает их локализацию и коррекцию. При этом используются коды Рида-Соломона с минимальным кодовым расстоянием d₀ = 5.

Сверточные коды

Кроме рассмотренных корректирующих кодов используются так называемые сверточные коды, контрольные биты, в которых формируются непрерывно из информационных и контрольных бит смежных блоков.

Выводы