Реферат: Колебания и волны
Маятником является всякое тело, подвешенное так, что его центр тяжести находится ниже точки подвеса. Молоток, висящий на гвозде, весы, груз на веревке – все это колебательные системы, подобные маятнику стенных часов.
У всякой системы, способной совершать свободные колебания, имеется устойчивое положение равновесия. У маятника это положение, при котором центр тяжести находится на вертикали под точкой подвеса. Если мы выведем маятник из этого положения или толкнем его, то он начнет колебаться, отклоняясь то в одну сторону, то в другую сторону от положения равновесия. Наибольшее отклонение от положения равновесия, до которого доходит маятник, называется амплитудой колебаний. Амплитуда определяется тем первоначальным отклонением или толчком, которым маятник был приведен в движение. Это свойство – зависимость амплитуды от условий в начале движения – характерно не только для свободных колебаний маятника , но и вообще для свободных колебаний очень многих колебательных систем.
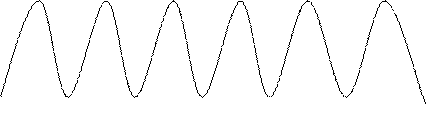
Прикрепим к маятнику волосок и будем двигать под этим волоском закопченную стеклянную пластинку. Если двигать пластинку с постоянной скоростью в направлении, перпендикулярном к плоскости колебаний, то волосок прочертит на пластинки волнистую линию. Мы имеем в этом опыте простейший осциллограф – так называются приборы для записи колебаний. Таким образом волнистая линия представляет собой осциллограмму колебаний маятника.
|
![]()
![]()
![]()
Амплитуда колебаний изображается на этой осциллограмме отрезком AB, период изображается отрезком CD, равным расстоянию, на которое передвигается пластинка за период маятника.
Так как мы двигаем закопченную пластинку равномерно, то всякое ее перемещение пропорционально времени, в течении которого оно совершалось. Мы можем сказать поэтому, что вдоль оси x в определенном масштабе отложено время. С другой стороны, в направлении, перпендикулярном к x волосок отмечает на пластинке расстояние конца маятника от его положения равновесия, т.е. путь пройденный концом маятника от этого положения.
Как мы знаем, наклон линии на таком графике изображает скорость движения. Через положение равновесия маятник проходит с наибольшей скоростью. Соответственно этому и наклон волнистой линии наибольший в тех точках, где она пересекает ось x. Наоборот, в моменты наибольших отклонений скорость маятника равна нулю. Соответственно этому и волнистая линия в тех точках, где она наиболее удалена от оси x, имеет касательную параллельную x , т.е. наклон равен нулю
Гармоническое колебание. Частота.
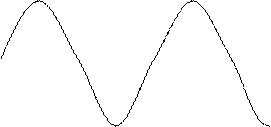
Колебание, какое совершает при равномерном движении точки по окружности проекция этой точки на какую-либо прямую, называется гармоническим (или простым) колебанием.
Гармоническое колебание является специальным, частным видом периодического колебания. Этот специальный вид колебания очень важен, так как он чрезвычайно часто встречается в самых различных колебательных системах. Колебание груза на пружине, камертона, маятника, зажатой металлической пластинки как раз и является по своей форме гармоническим. Следует заметить, что при больших амплитудах колебания указанных систем имеет несколько более сложную форму, но они тем ближе к гармоническому, чем меньше амплитуда колебаний.
| |
|

![]()
![]()
![]()
![]()
![]()
|
???? ?? ?????????????? ??? ??????????? ??????????? ????
Число циклов гармонического колебания, совершаемых за 1с, называется частотой этого колебания. Единицу частоты называют герцем. (Гц)
?????? ????????? ????????????????? ??????? , ?????????? ? ????????, ????? T , ? ???????, ?????????? ? ??????, ????? v , ????? ?????
Динамика гармонических колебаний.
Рассмотрим динамику свободных колебаний в идеальных колебательных системах без трения.
Отведем шар пружинного маятника от положения равновесия. В этом случае на шар действует возвращающая сила, направленная в сторону положения равновесия.
Ее проекция имеет знак, противоположный знаку смещения x
?????????? ??????? ???? ? ?????? ??????????????? ????????. ??????? ??????? ?? ????????? ??????????. ? ???? ?????? ???????????????? ???? ??????? ? ???? ????????? ???? ?????????? ? ??????? ????????? ??????????. ??? ???? ????? ???????? ???:
?? ???? ????????????? ????????? ? ?????????? ?????? ??????????, ??
так как ![]() . Величина
. Величина ![]() постоянна. Обозначим ее через k. Тогда
постоянна. Обозначим ее через k. Тогда
?????????? ???? ? ??????? ??????????????? ????????.
Превращения энергии при свободных колебаниях.
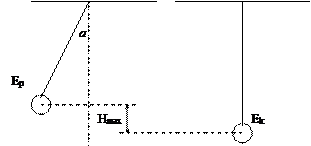 |
Отведем маятник на небольшой угол a от положения равновесия. Этим мы сообщим маятнику потенциальную энергию:
??? Hmax ? ???????????? ?????? ??????? ????????.
???????? ???????. ??? ????????? ???? ??????? ? ???? ??????? ???????? ????? ????????? ? ????????? ??????????. ??? ???? ??? ????????????? ??????? ???????????? ? ????????????. ? ????????? ?????????? ??? ?????????? ???????? ????????????? ??????? ??????????? ? ????????????: