Реферат: Компьютерное моделирование в экологии

Как уже было сказано, скорость роста зависит от концентрации биогенных веществ. Для фитопланктона элементами, способными лимитировать рост, могут являться, например, азот, фосфор и углерод. Возможные способы отражения этого факта в работе С.Йоргенсена описаны следующим образом

,

где P, N, C – концентрация растворенного фосфора, азота и углерода; K_P , K_N , K_С – соответствующие константы полунасыщения. Возможно также использование средней величины лимитирующих факторов: .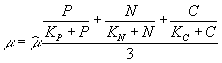

В работах Н.С.Абросова с коллегами была предложена следующая модель динамики экосистемы. Рассматривают организмы одного трофического уровня, которые существуют за счет совместного потребления ресурсов питания. Пусть  _ij (s¹ ,...,s^m ) – скорость потребления единицей биомассы (особью) вида i ресурса j ;  _i =  _i (s¹ ,...,s^m ) – удельная скорость прироста биомассы (плотности) i -го вида; s = (s¹ ,...,s^m ) – вектор концентрации ресурсов в среде; d_i – удельная скорость элиминации организмов i -го вида; А^j – скорость поступления j -го субстрата извне на единицу объема экосистемы; Dⁱ – удельная скорость удаления ресурса в открытой системе. Тогда динамика системы описывается уравнениями

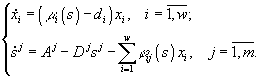(1)

Модель, описывающая культивируемое в хемостате сообщество, является частным случаем модели (3.1) при условиях dⁱ = D^j = D , = A^j /D , где D – скорость разведения культуры, – концентрация j -го субстрата в поступающей в реактор питательной среде, и задается системой уравнений

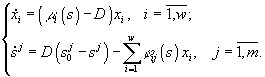
(Хемостат – непрерывный культиватор, в котором за счет саморегулирующх механизмов популяции поддерживается постоянная плотность популяции.)

В случае взаимозаменяемых ресурсов зависимость  _i (s ) описывается выражением

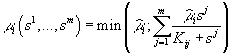
или его линейной аппроксимацией

,

где  _ij – элементы матрицы приспособленности: , здесь  _ij = c_ij Y_ij , где c_ij – удельная скорость потребления j -го субстрата i -м видом организма, а Y_ij – экономический коэффициент использования j -го вещества i -м видом.

Если ресурсы взаимонезаменяемы, то

или

.

В приведенных выше формулах символ обозначает максимально возможную удельную скорость роста организмов i -го вида; K_ij – константа полунасыщения роста i -го вида на j -м субстрате.

В моделях, использующих дифференциальные уравнения, возможен учет лимитирования роста световой энергией. В этом случае предлагается использовать следующую зависимость:

здесь x_i – концентрация клеток i -го вида; μ_i – удельная скорость роста i -го вида; – максимально возможная удельная скорость роста организмов i -го вида; – процентное содержание хлорофилла в биомассе; l_i – коэффициент поглощения света i -м видом; – КПД фотосинтеза i -го вида клеток; Y_i – величина, обратная калорийности биомассы i -го вида клеток; E – мощность ФАР (фотосинтетически активной радиации), падающей на поверхность культуры; d – толщина слоя культуры в кювете культиватора (приведено выражение для удельной скорости μ_i в случае лимитирования совместного роста двух видов только энергией света) (Абросов, Ковров, 1977).

А.Я.Болсуновским (1999) была предложена следующая математическая модель динамики компонентов сообщества из двух видов (спирулина и хлорелла), рост которых лимитируется интенсивностью света всей области ФАР

где x_i – концентрация клеточного хлорофилла; μ_i – удельные скорости роста; a_i , b_i – константы уравнения Михаэлиса-Ментен; – средняя освещенность для всего сообщества; E₀ – поверхностная освещенность; D – скорость протока.

Кроме того, в моделях возможно отразить эффекты метаболического воздействия, как, например, это было сделано Ю.А.Домбровским с соавторами (1990). Скорость роста фитопланктона i -го вида описывалась выражением

,

где x₁ , x₂ , s – концентрации двух видов фитопланктона и минерального вещества, выраженные в единицах лимитирующего биогенного вещества; – коэффициенты метаболизма; M_i – максимальная скорость фотосинтеза; H_i – параметр насыщения; – эмпирический коэффициент ингибирования i -го вида j -м.

Как уже указывалось выше, при моделировании динамики биомассы фитопланктона, чаще всего используют уравнение Моно, описывающее зависимость удельной скорости роста популяции μ от концентрации s лимитирующего рост субстрата

, (2)