Реферат: Консолидирование задолженности

1 + n1 i0 1 + n2 i0

Находим

(1)

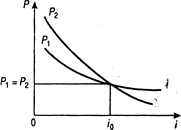
рис. 1.

Из формулы (1) следует, что чем больше различие в сроках, тем больше величина i0 при всех прочих равных условиях. Рост отноше­ния S1/S2 оказывает противоположное влияние.

Если дисконтирование производится по сложной ставке, то кри­тическую ставку найдем из равенства

S1 (1+ i0) = S2 (1+ i0)

Получим:

(2)

Принцип эквивалентности приме­няется при различных изменениях условий выплат денежных сумм.

Общий метод решения подобного рода задач заключается в разра­ботке так называемого уравнения эквивалентности, в котором сумма заменяемых платежей, приведенных к какому-ли­бо моменту времени, приравнивается к сумме платежей по новому обязательству, приведенных к той же дате. Для краткосрочных обя­зательств приведение осуществляется обычно на основе простых ставок, для средне- и долгосрочных — с помощью сложных ставок. Заметим, что в простых случаях часто можно обойтись без специаль­ной разработки и решения уравнения эквивалентности.

Одним из распространенных случаев изменения условия являет­ся консолидация (объединение) платежей. Пусть платежи S1, S2, …, Sm со сроками n1, n2, …, nm заменяются одним в сумме So и сроком n0. В этом случае возможны две постановки задачи: если задается срок n0, то находится сумма So, и наоборот, если задана сумма консоли­дированного платежа So, то определяется срок n0.

При определении суммы консолидированного платежа уравнение эквивалентности имеет простой вид. В общем случае, когда n1< n2, <…<. nm , причем n1< n0 < nm , искомую величи­ну находим как сумму наращенных и дисконтированных платежей. При применении простых процентных ставок получим:

(3)

где Sj — размеры объединяемых платежей со сроками ni< n0;

Sk - размеры платежей со сроками n k > n0;

В частном случае, когда n0 > nm

(4)

При объединении обязательств можно применить и учетные ставки. В этом случае при условии, что все сроки выплат пролон­гируются, т.е. n0 > nj , находим сумму наращенных по учетной став­ке платежей:

So = å Sj (1- tj d )

В общем случае имеем

So = å Sj (1- tj d ) + å Sk (1- tk d )

Здесь tj, tk имеют тот же смысл, что и выше.

Консолидацию платежей можно осуществить и на основе слож­ных ставок. Вместо формулы (3) получим для общего случая

( n1 < nо< nm )

So = å Sj (1+ t ) + å Sk (1 + i ) (5)

Если при объедине­нии платежей задана величина консолидированного платежа So, то возникает проблема определения его срока n0. В этом случае урав­нение эквивалентности удобно представить в виде равенства совре­менных стоимостей соответствующих платежей.

При применении простой ставки это равенство имеет вид:

So (1+ n0i ) = å Sj (1+ nj i )

Отсюда

(6)

Очевидно, что решение может быть получено при условии, что Sо > å Sj (1+ nj i )

Иначе говоря, размер заменяющего платежа должен быть больше суммы современных стоимостей заменяемых пла­тежей. Искомый срок пропорционален величи­не консолидированного платежа.

При консолидации платежей на основе сложных про­центных ставок уравнение эквивалентности будет следующим:

So (1 + i) = å Sj (1+ i )

Для упрощения дальнейшей записи можно принять:

Q = å Sj (1+ i )

Тогда

(7)

Решение существует, если соблюдено условие So > Q. Для частного случая, когда Sо = å Sj при определении срока кон­солидирующего платежа вместо формулы (7) иногда применяют средний взвешенный срок:

(8)

Привлекательность этой формулы, помимо ее простоты, состоит в том, что она не требует задания уровня процентной ставки. Она дает приближенный результат, который больше точного. Чем выше ставка i, тем больше погрешность реше­ния по формуле (8).