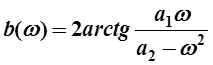Реферат: Коррекция частотных искажений сигналов

При решении задачи аппроксимации по вполне очевидным причинам естественным будет выбор чебышевского критерия близости, котороый в данном случае имеет вид:

,

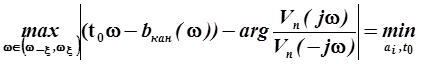где a_i - коэффициенты полинома V_n ( jω ) Гурвица, t ₀ - время, определяемое из условий допустимой задержки сигнала.

С алгоритмом и программой решения этой задачи можно ознакомиться в технической литературе.

Найденную Т(р) представляют в виде функции - сомножителей первого и второго порядка, необходимую для каскадной реализации ФК.

Схемы и характеристики фазовых звеньев.

Пассивные фазовые звенья обычно реализуются в виде мостовых или Т-образных перекрытых четырехполюсников. Если в результате аппроксимации определена Т(р) фазового корректора, то сопротивление двухполюсников и мостовой схемы весьма просто найти по ранее полученным формулам при .

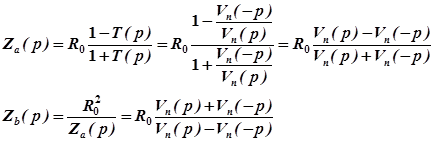
Осуществим реализацию звена 1-го порядка, для которого

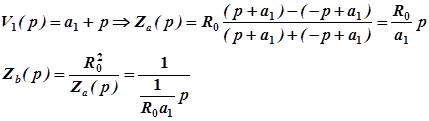
Нетрудно определить (путем замены Р= j w ), что Z_a ( jω ) представляет собой индуктивность L_a = R ₀ / a ₁ , а Z_b ( jω ) - емкость C_b =1/ R ₀ a ₁ .

Затухание такого звена

,

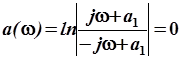а рабочая фаза

.

Мостовая схема и график b(w) показана на рисунке 7.

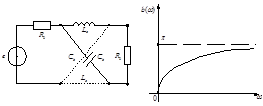
Рисунок 7.

В связи с известными недостатками мостовой реализации, на практике используют четырехполюсники эквивалентные мостовым. Одной из таких схем может быть схема с идеальным трансформатором (рисунок 8а.)

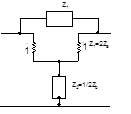
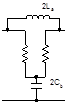
а) б)

Рисунок 8.

Таким образом, для фазового звена 1-го порядка получается схема, представленная на рис.8.б.

Действуя аналогичным образом, можно получить схемы фазовых звеньев 2-го порядка.

Для мостовой схемы:

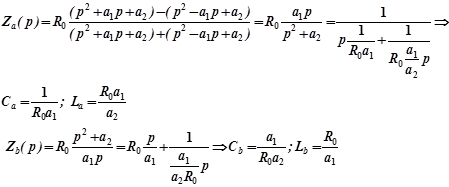
Видно, что Z _a ( p ) представляет собой параллельное, а -последовательное соединение элементов L и C .

При этом