Реферат: Курсовая работа по теории электрических цепей
Для схемы:
U0 (t)= U0 =constU0 =5 В
i0 (t)=I0 d1 (t) I0 =2 A
1.1 Составить уравнения состояния для цепи при t ³ 0.
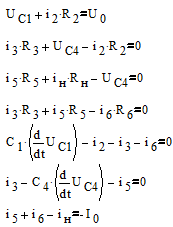Переменными состояния для данной схемы будут являться напряжения на емкостях С1 и С4 . Для нахождения уравнений состояния запишем уравнения по I и II законам Кирхгофа:
(1)
Для нахождения производных переменных состояния решим следующую систему, полученную из системы (1), приняв за неизвестные все токи, участвующие в системе (1) и первые производные переменных состояния. Переменные состояния примем за известные величины для получения их в правой части уравнений состояния:
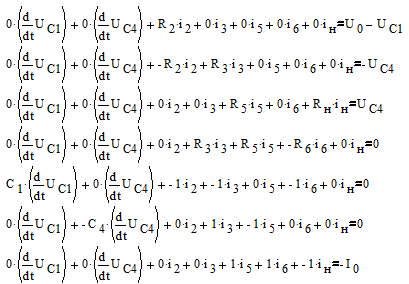
(2)
Решаем эту систему в матричном виде с помощью MathCad:
Таким образом, уравнения состояния будут иметь вид:
 |
1.2 Найти точные решения уравнений состояния.
Сначала найдем корни характеристического уравнения как собственные числа матрицы, составленной из коэффициентов при переменных состояния в уравнениях состояния:
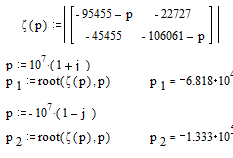
Общий вид точных решений уравнений состояния:
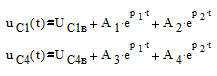
Вынужденные составляющие найдем как частное решение уравнений состояния, учитывая то, что если в цепи включены только постоянные источники питания, значит, и принужденные составляющие будут константами, соответственно производные принужденных составляющих будут равны нулю. Учитывая выше сказанное, найдем их из уравнений состояния следующим способом:
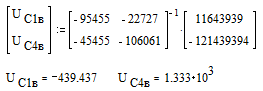
Начальные условия (находятся из схемы):
Для нахождения постоянных интегрирования A1 , A2 , A3 , A4 требуется 4 уравнения. Первые два уравнения получим из выражений точного решения уравнений состояния, учитывая законы коммутаций: переменные состояния не меняют своего значения в момент коммутации.
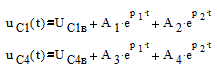
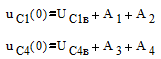
При t=0:
Далее найдем значения производных переменных состояния при t=0 из уравнений состояния:
Выражения эти производных найденные из выражений решения уравнений состояния:
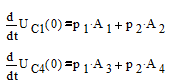
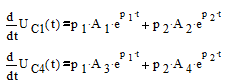
При t=0:
Таким образом имеем 4 уравнения для нахождения постоянных интегрирования, находим их:
Точные решения уравнений состояния:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--