Реферат: Кватернионы
j -k -1 i
k -j -i -1
По определению операции сложения и умножения кватернионов производятся по обычным правилам раскрытия скобок и приведения подобных членов с учетом правил (5) – (6).
Согласно этому определению, если и – два кватерниона, то
![]()
![]() (7)
(7)
Это, разумеется, привычное нам “покоординатное” сложение. Далее, произведение кватернионов и вычисляется так:
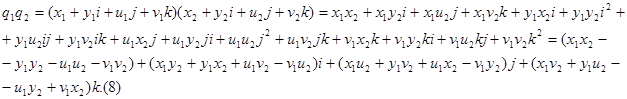
Длинная, но совершенно автоматическая проверка показывает, что умножение кватернионов обладает сочетательным свойством:
Естественно считать, что действительные и комплексные числа являются частным случаем кватернионов. Так, действительное число x – это кватернион вида
Комплексное число z = x + yi представляется как кватернион
У операции сложения кватернионов, очевидно, имеется обратная операция –вычитание. Именно, разность двух кватернионов и определяется формулой:
Если , то разность кватернионов – это нулевой кватернион.
Деление кватернионов
Перейдем теперь к операции деления кватернионов, обратной к операции умножения. Вообще, что мы понимаем под частным от деления числа a на число b , не равное нулю? Это такое число c, что
bc = a. (10)
Так определяется частное от деления для действительных и комплексных чисел. К сожалению, для кватерниона применить непосредственно это определение мы не можем. Для того чтобы формула (10) “корректно” определяла частное, нужно, чтобы произведение не зависело от порядка сомножителей. В противном случае наряду с частным определенным формулой (10), существует вполне равноправное “левое” частное” с’, определяемое формулой
c’b = a,
которое может отличаться от “правого частного” c из (10). Вот здесь, кроме необходимости выйти за пределы трехмерного пространства, Гамильтону пришлось принести еще одну жертву.
Оказывается, определенные им новые числа – кватернионы – потеряли еще одно привычное качество: произведение кватернионов зависит от порядка сомножителей. Действительно, уже в формулах (6) при изменении порядка сомножителей произведение меняет знак.
Таким образом, можно говорить лишь о “делении справа” и “делении слева”. Как реально найти, скажем, “левое частное” от деления кватерниона на кватернион ?
Обозначим искомое частное через q = x + yi + uj + vk . Тогда, используя правило умножения для кватернионов и определение левого частного, получим следующее равенство кватернионов:
,
или
![]()
Полученное равенство равносильно системе четырех линейных уравнений с переменными x, y, u, v :
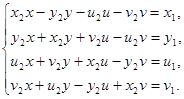
Аналогичным образом находится “правое частное” от деления на .
Рассмотрим частный случай, когда делимое равно единице. В этом случае частное от деления =1 на кватернион (и “слева” и “справа”) равно одному и тому же кватерниону
Поэтому кватернион p обозначается через . Тогда “правое частное” от деления кватерниона на выражается формулой
,
а “левое частное” от деления кватерниона на – формулой
Практически частное от деления двух кватернионов ищется другим путем. Для этого нам потребуются
Скалярные и векторные кватернионы