Реферат: Лабораторная работа

В предыдущих лабораторных работах была изложена теория многочленной аппроксимации. Попробуем теперь изложить подобную теорию для аппроксимации периодических функций рядами Фурье. Ряд Фурье на интервале -N£t£N можно записать так:

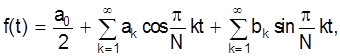
где 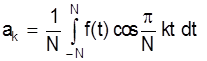(k=0, 1, 2, …)

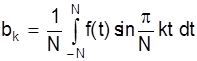(k=0, 1, 2, …)

1 -p 0 p -1

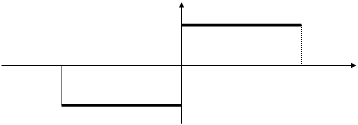
В качестве примера рассмотрим разложение прямоугольного колебания в ряд Фурье. Подобное колебание, называемое меандром, находит широкое применение в технике. Итак,

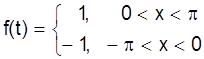
Так как на практике мы не можем вычислить бесконечную сумму, проанализируем, как увеличение числа слагаемых влияет на приближение. При этом мы сталкиваемся с явлением Гиббса.

H(t) 0 p 2p 3p t Прямоугольная

Рассмотрим это явление на примере прямоугольной волны H(t) с периодом 2p.

Если вычислить сумму первых 2n членов, то все члены с косинусами будут равны нулю и получаем: -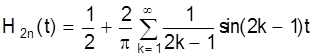

H2n (t) H(t) 1 ½ явление Гиббса p t

Гиббс отметил, что частичная сумма H_2n превосходит функцию на некоторую величину. Более точно

H_2n 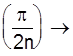1,08949…, при n®¥

Действительно, H_2n (t) не только превосходит функцию H(t), но и имеет тенденцию колебаться около H(t), и колебания уменьшаются медленно, когда t удаляется от разрыва.

Чтобы объяснить явление, запишем - как -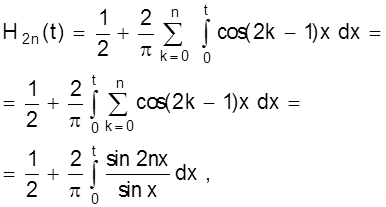

где использована формула

Из выведенной формулы - ясно, что максимум и минимум для 0£t£p достигаются в точках ,

--> ЧИТАТЬ ПОЛНОСТЬЮ <--