Реферат: Лабораторный практикум

0

1

1

1

1

1

0

1

0

0

Рассмотрим теперь процессы, которые будут происходить в схеме при подаче входного набора xy=01. Будем считать для определенности, что в момент подачи этих сигналов на выходе был уровень z=1. Примем, что время задержки у всех логических элементов одинаково и равно t. Тогда через время t на выходах

элементов D₁ и D₂ одновременно установится сигнал 0. Через время 2t на выходе элемента D₃ установится сигнал 1, а через время 3t на выходе z установится сигнал 0 и т.д., т.е. на выходе схемы будут происходить изменения сигнала с 0 в 1 и с 1 в 0. Учтем, что на входе комбинация сигналов (xy=01) при этом не изменяется.

Таким образом, в этой схеме будут происходить колебания с периодом 6t.

При малой величине t (большой частоте) колебания могут сорваться из-за того, что передача сигнала при такой частоте будет происходить без восстановления уровня (без усиления). В этом случае на выходе установится некоторая промежуточная нестандартная амплитуда сигнала. Аналогичная ситуация будет иметь место, если правую часть уравнения (1) реализовать на элементах (диодах) типа ИЛИ и И, не обладающих свойством восстановления уровня сигнала.

Следовательно, логическая схема с обратной связью в зависимости от комбинации входных сигналов может быть конечным автоматом или вообще будет неправильно функционировать (выдавать нестандартный сигнал, либо генерировать колебания).

Однако схемы с обратной связью, имеющие много входов и выходов, анализировать подобным образом трудно, т.к. таблицы согласования в форме таблицы истинности становятся очень громоздкими. В таком случае используют другую форму таблицы соответствия, а именно, карту Карно. Строго определенный порядок перечисления переменных облегчает отображение на картах Карно кодировки внутренних состояний и их устойчивости, что обуславливает удобство использования этого вида карт для анализа и синтеза последовательностных схем.

Рассмотрим конкретный пример анализа логической ячейки типа И-НЕ, охваченной обратными связями (рисунок 2). Эта схема (и подобные другие) получили название бистабильных ячеек (БЯ).

Анализ БЯ будем проводить поэтапно по следующей методике:

2.1 Запишем логические уравнения выходов схемы

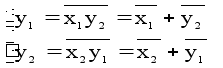. (2)

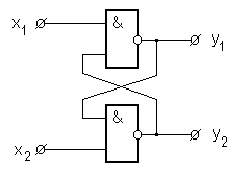
Рисунок 2 - Бистабильная ячейка типа И-НЕ

2.2 Составим карту Карно, при помощи которой будем решать эту систему.

Столбцы этой карты обозначим всевозможными комбинациями независимых (входных) переменных x₁ и x₂, а строки - комбинациями зависимых (выходных) переменных y₁ и y₂ (таблица 2). В клетки этой карты запишем истинные значения функций y₁ и y₂, определенные в соответствии с приведенной системой уравнений (2). Таким образом, в клетках будет записано двузначное двоичное число, при этом первый разряд будет соответствовать значению y₁, а второй разряд этого числа - значению y₂.

??????? 2 - ??????? ?????????? ??????? 3 - ???????

?????????

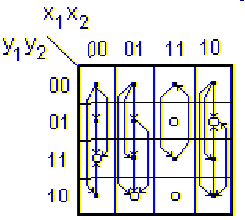
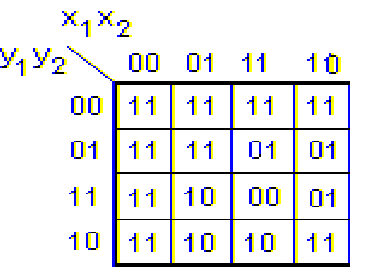
Очевидно, что состояние схемы является устойчивым, если значения функций y₁ и y₂ совпадают с обозначением соответствующей строки таблицы.

Например, при пересечении столбца 01 и строки 10 находится устойчивое состояние 10, а на пересечении того же столбца и строки 11 - неустойчивое состояние 10.