Реферат: Лазерная резка : расчет зануления кабельной сети и освещенности сборочного мест блока

Практическое использование разрушения металлов посредством механизма испарения затруднено в связи с достаточно высокими энергозатратами на теплопроводность материала и необходимостью поддержания температуры металла на уровне температуры кипения.

Заметное снижение энергозатрат достигается использованием вспомогательного газа для удаления продуктов разрушения металла из канала реза.

Процесс нагрева поверхности материала лазерным излучением при отсутствии фазовых переходов описывается уравнениями ( 1.1, 1.2 ).

Падающее излучение поглощается в тонком приповерхностном слое по закону Буггера:

q_{( x )} = a Ч q_o Ч exp( -x Ч x ); ( 1.1 )

где: q_{( x )} - плотность потока лазерного излучения, Вт/см²;

a - поглощательная способность материала;

a Ч q₀ - плотность лазерного потока поглощенная поверхностью;

x - коэффициент поглощения излучения в

материале, см^-1.

Глубина проникновения излучения в вещество составит: l = 1/x . Для металлов величина x составляет 10⁴ - 10^-5 см^-1.

Распространение теплового потока описывается законом Фурье:

( 1.2 )

где: f - тепловой поток, Вт/см²;

l - коэффициент теплопроводности, Вт/(С⁰ Ч см) ;

Т - температура, С⁰.

Уравнение теплопроводности при нагреве движущихся образцов. Для описания температурных полей, возникающих при лазерной резке металлов, используется уравнение теплопроводности. Это уравнение формирует условия теплопередачи в твердых телах вследствии теплопроводности.

В общем случае уравнение теплопроводности является нелинейным. Лишь для некоторых частных случаев изменений теплофизических свойств материала, c_(Т) - удельной теплоемкости материала [ Дж/(гЧС⁰)], а_(Т) - коэффициента температуропроводности [ см²/c ], l - коэффициента теплопроводности [ Вт/(C⁰Чсм)], задаваемых в виде упрощенных аналитических зависимостей, можно получить сложные аналитические выражения.

В большинстве практических случаев воздействия лазерного излучения на металл, для инженерных расчетов важным обстоятельством является возможность упрощенного аналитического описания процессов распространения теплоты.

Наличие аналитических зависимостей упрощает анализ тепловых процессов, позволяет оперативно устанавливать закономерности резки.

С целью получения аналитического решения вводят некоторые упрощения параметров теплопередачи. Принимают, что теплофизические свойства материала, такие как, c - удельная теплоемкость материала, а - коэффициент температуропроводности, l - коэффициент теплопроводности и a - коэффициент поглощения материала, не зависят от температуры.

Приближенно нагрев элемента объема происходит за время прохождения луча над этим объемом: t = 2R/n, за это время волна теплопроводности уйдет на глубину, равную ( а Ч t)^1/2 .

Условием многомерного распределения тепла можно считать, что распространение волны теплопроводности вглубь материала значительно больше радиуса луча RЧ t )^1/2, ???

Rn/a > 1. 1.3

В случае, когда излучение фокусируется в пятно с радиусом R = 0,01 см при обработке алюминия а = 0,91 см²/с скорость перемещения луча n < 100 см/с, это будет являться условием медленно движущегося образца, согласно (1.3).

Для случая медленно движущегося образца преобразовывая уравнения (1.1 и 1.2) температура поверхности составит:

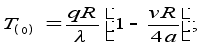1.4

где: q - плотность мощности лазерного излучения;

a - коэффициент поглощения;