Реферат: Лекции по физике В.И.Бабецкого
Ну и сразу такое определение:при достаточно хорошей симметрии напряжённость поля может быть найдена из уравнения ![]() . Значит, при достаточно хорошей симметрии поле всегда может быть найдено вот из этой интегральной теоремы. Ну, у нас это первое уравнение Максвелла. А теперь частные случаи.
. Значит, при достаточно хорошей симметрии поле всегда может быть найдено вот из этой интегральной теоремы. Ну, у нас это первое уравнение Максвелла. А теперь частные случаи.
1) Центральная (сферическая) симметрия. Пусть плотность заряда ![]() есть
есть ![]() . Значит, плотность, которая, вообще, функция координат точки
. Значит, плотность, которая, вообще, функция координат точки ![]() , зависит только от
, зависит только от ![]() , то есть только от расстояния до начала координат, это означает, что начало координат – центр симметрии. Вот эта формулка
, то есть только от расстояния до начала координат, это означает, что начало координат – центр симметрии. Вот эта формулка ![]() =
=![]() означает, что плотность на любой сфере радиуса r – константа, какая-то там плотность, ну, и отличная от нуля, на любой сфере она постоянна. Это означает, что распределение обладает сферической симметрией, и создаваемое им поле будет также обладать сферической симметрией. Отсюда следует, что
означает, что плотность на любой сфере радиуса r – константа, какая-то там плотность, ну, и отличная от нуля, на любой сфере она постоянна. Это означает, что распределение обладает сферической симметрией, и создаваемое им поле будет также обладать сферической симметрией. Отсюда следует, что ![]() (потенциал как функция точки) это есть
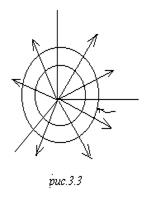
(потенциал как функция точки) это есть ![]() . Отсюда эквипотенциальные поверхности – сферы с центром в начале координат , то есть вот на любой сфере потенциал – константа. Отсюда далее следует, что силовые линии поля, которые являются всегда ортогональными к эквипотенциальным поверхностям, силовые линии поля – вот такие радиальные лучи:
. Отсюда эквипотенциальные поверхности – сферы с центром в начале координат , то есть вот на любой сфере потенциал – константа. Отсюда далее следует, что силовые линии поля, которые являются всегда ортогональными к эквипотенциальным поверхностям, силовые линии поля – вот такие радиальные лучи:
![]()
![]() Конструкция электрического поля может быть только такая. А теперь заметьте, здесь никакой специфики электричества не было, все эти выводы получены только из соображений симметрии. Любое векторное поле имело бы такую структуру, какая бы физическая природа у него ни была. Только сила соображения симметрии очень часто позволяет делать выводы безотносительно к конкретному предмету разговора.
Конструкция электрического поля может быть только такая. А теперь заметьте, здесь никакой специфики электричества не было, все эти выводы получены только из соображений симметрии. Любое векторное поле имело бы такую структуру, какая бы физическая природа у него ни была. Только сила соображения симметрии очень часто позволяет делать выводы безотносительно к конкретному предмету разговора.
![]() =
=![]() , отсюда дальше следует, что напряжённость поля на любой сфере
, отсюда дальше следует, что напряжённость поля на любой сфере ![]() может быть представлен так:
может быть представлен так: 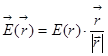 . Вот это
. Вот это ![]() , радиус-вектор, делённый на собственный модуль, есть единичный вектор
, радиус-вектор, делённый на собственный модуль, есть единичный вектор ![]() в направлении радиус-вектора. Всё. Пишем дальше эту формулу
в направлении радиус-вектора. Всё. Пишем дальше эту формулу ![]() . В качестве замкнутой поверхности, которая фигурирует в интеграле (поток вычисляется по замкнутой поверхности), выбираем сферу
. В качестве замкнутой поверхности, которая фигурирует в интеграле (поток вычисляется по замкнутой поверхности), выбираем сферу ![]() . Мы её (поверхность) можем брать любой, равенство от этого не зависит, но удобно взять
. Мы её (поверхность) можем брать любой, равенство от этого не зависит, но удобно взять ![]() . Пишем:
. Пишем:  . Это равенство вследствие того, что
. Это равенство вследствие того, что ![]() ,
, ![]() - единичный вектор в направлении радиус-вектора (это вектор нормали к сфере, но нормаль к сфере в данной точке совпадает по направлению с радиус-вектором данной точки, эти векторы параллельны), а проекция радиус-вектора на самого себя – это его модуль, конечно,
- единичный вектор в направлении радиус-вектора (это вектор нормали к сфере, но нормаль к сфере в данной точке совпадает по направлению с радиус-вектором данной точки, эти векторы параллельны), а проекция радиус-вектора на самого себя – это его модуль, конечно, ![]() . Дальше,
. Дальше, ![]() во всех точках сферы одно и тоже, выносим за знак интеграла:
во всех точках сферы одно и тоже, выносим за знак интеграла: ![]() (вот это всё была математика, она к физике никакого отношения пока не имела, а физика – это следующее равенство), эта величина должна равняться интегралу от плотности заряда по объёму сферы, по которой вычисляется поток (интеграл от плотности по объёму это есть полный заряд внутри сферы):
(вот это всё была математика, она к физике никакого отношения пока не имела, а физика – это следующее равенство), эта величина должна равняться интегралу от плотности заряда по объёму сферы, по которой вычисляется поток (интеграл от плотности по объёму это есть полный заряд внутри сферы): ![]() , где
, где ![]() – заряд внутри сферы радиуса
– заряд внутри сферы радиуса ![]() . И это утверждение верно для сферы любого радиуса. Отсюда вывод – при центральной симметрии напряжённость поля во всех точках сферы радиуса
. И это утверждение верно для сферы любого радиуса. Отсюда вывод – при центральной симметрии напряжённость поля во всех точках сферы радиуса ![]() равна:
равна:
![]() ,
,
где ![]() - единичный вектор нормали к сфере. Эта формула, одна единственная, добивает все задачи центральной симметрии. Проблема одна – найти заряд, который находится внутри данной сферы, ну, это не очень тяжёлая проблема.
- единичный вектор нормали к сфере. Эта формула, одна единственная, добивает все задачи центральной симметрии. Проблема одна – найти заряд, который находится внутри данной сферы, ну, это не очень тяжёлая проблема.
Можем немножко продолжить это дело. Вследствие того, что на любой сфере ![]() , интеграл по объёму можно свести, в принципе, к однократному интегралу, интегрируя по шаровым слоям, ну, напишу тут без подробных комментариев
, интеграл по объёму можно свести, в принципе, к однократному интегралу, интегрируя по шаровым слоям, ну, напишу тут без подробных комментариев  . Вот это
. Вот это ![]() объём шарового слоя радиуса
объём шарового слоя радиуса ![]() толщиной
толщиной ![]() . Почему я тут штрихи поставил, понятно.
. Почему я тут штрихи поставил, понятно. ![]() стоит в верхнем пределе интеграла, ну тогда, чтоб не путать переменную интегрирования с верхним пределом, там я вместо
стоит в верхнем пределе интеграла, ну тогда, чтоб не путать переменную интегрирования с верхним пределом, там я вместо ![]() пишу
пишу ![]() . Значит, если вот эта функция
. Значит, если вот эта функция ![]() предъявлена, то такой интеграл вычисляется. Так, всё, с центральной симметрией конец. Второй случай.
предъявлена, то такой интеграл вычисляется. Так, всё, с центральной симметрией конец. Второй случай.
![]()

![]()
![]()