Реферат: Лобачевский и неевклидова геометрия

3. Из любого центра можно провести окружность любым радиусом.

4. Все прямые углы равны между собой.

Пятый постулат является своеобразным философским камнем геометрии и будет подробнее описан в шестой части.

Биография Николая Ивановича

Лобачевского.

1729 – 1856

Детство Лобачевского было тяжелым и бедным. В Казанской гимназии он был казеннокоштным студентом, что накладывало определенные обязанности и ограничения. Самым простым было учиться лучше других; но казеннокоштным студентам, например, не разрешалось выходить дальше, чем за пределы парадного двора. Но уже с самого начала жизни Лобачевский интересовался геометрией. Это неудивительно, ведь его отец был землемером. Лобачевский проявил также большую склонность к языкам – например, французский он выучил за три месяца. Он писал стихи – его поэмы о Волге считаются одними из лучших. Но при этом он не забывал учиться – в 1807 году он студент, а в 1811 – магистр. Работая над развитием геометрии, в 1826 году, уже будучи деканом физико-математического факультета, он сделал доклад, содержавший основы неевклидовой геометрии. Однако время было не совсем подходящим: открылись хищения из казны Магницким – ещё одним математиком этой эпохи, Магницкого «записали» в декабристы… Словом, ученому миру было не до новых теорий.

Но он не сдался. С 1829 по 1830 год он публиковал в журнале «Казанский вестник» мемуар «О началах геометрии», и это была первая публикация основ его теории.

Взлеты и падения следовали один за другим. Только были сданы в печать первая и вторая части «Новых начал геометрии», как умер его кумир Пушкин, а потом и дочь Надежда.

Лобачевский пользовался уважением и любовью студентов и коллег. Когда упразднили должность директора университета, то его кандидатуру на пост главного ректора утвердили без возражений. Не высказался даже его главный соперник – Симонов.

в 1842 году, во время большого пожара в Казани он героически спас древние книги, до этого, во время эпидемии холеры, превратил университет в мини-госпиталь – из-за чего умерло гораздо меньше студентов, чем в других ВУЗ’ах.

Когда негде было разместить второй класс Казанской гимназии, он предложил свой дом, обещав потом построить для гимназии дворец. Понятно, что в 1845 году он получил должность управляющего Казанским учебным округом, а после стал член-кореспондентом Гуттенгенского университета.

Но жизнь нанесла ещё один удар: он начал слепнуть. Он начал играть со своей женой в страшную игру, пытаясь убедить её, что ещё хорошо видит. Она закатывала истерики, уговаривала лечиться, но все тщетно – Лобачевский ослеп. Но, тем не менее, он продолжал преподавать и пользоваться безграничной любовью и уважением учеников. Знаменателен случай, когда молодого студента, засмеявшегося над споткнувшимся Лобачевским, однокурсники заставили уйти из университета. Лобачевский об этом даже не узнал.

В 1855 году он был уволен со службы с причислением к министерству. В этом же году опубликовал свою последнюю работу – «Пангеометрия», которую диктовал своим ученикам. Его горячим желанием было создать единую механику – но времени не хватило. Он умер в 1856 году – забытый царем, лишившись орденов и квартиры – ордена украли, а квартиру конфисковали. В его формулярном листе за сорок лет работы в графе отпусков бисерным почерком Лобачевского было написано: «Не был».

Ему поставлен памятник – и поэт В. Фирсов написал о нем:

Высокий лоб, нахмуренные брови,

В холодной бронзе – отраженный луг…

Но даже неподвижный и суровый,

Он, как живой, - спокоен и могуч.

Когда – то здесь, на площади широкой,

Задумчивый, неторопливый, строгий,

Он шел на лекции – великий и живой.

Пусть новых линий не начертят руки,

Он здесь стоит, взнесенный высоко,

Как утверждение бессмертья своего,

Как вечный символ торжества науки.
Другие авторы.

Идея неевклидовой геометрии пришла в голову не только Лобачевскому – просто ему относительно повезло. Одним из «конкурентов» был Гаусс – великий затворник, отказавшийся от услуг почты, чтобы никто не смог обвинить его в плагиате.

В это время сын старого друга Гаусса, Янош Больяи, занялся теорией параллельных линий. В 1832 году он выпустил труд «Аппендикс», содержащий начала неевклидовой геометрии. Но его работа почти совпадала с мемуаром Лобачевского «О началах геометрии» 1829 года; подобных результатов достиг и сам Гаусс.

Тога Гаусс написал Фаркашу Больяи то, что тот сам говорил сыну: время для этих выкладок ещё не пришло. Януш же посчитал, что Гаусс решил присвоить его труд. Но Гаусс не публиковал его – ведь он был королем математики того периода, и боялся, что его сочтут свихнувшимся.

Гаусс в то время хотел уехать – куда-нибудь далеко, где никто не помешает. Он думал о Петербурге или Казани. Но из-за бюрократии российских чиновников поездка расстроилась.

Но если Януш Больяи считал себя гением-одиночкой, то Гаусс узнал о Лобачевском, прочитав «Геометрические исследования по теории параллельных линий Николая Лобачевского». Гаусс говорил, что, читая этот труд, он видел в первую очередь себя. Гаусс закончил затворничество, начал изучать русский язык – и стал бегло читать уже через два месяца. Но – ирония судьбы – Гаусс стеснялся открыто попросить сочинения Лобачевского, а тот не отсылал их в Геттинген, так как не знал, что Гаусс понимает по-русски.

Через шесть лет Гаусс все ещё думает о Лобачевском. Но он понимает, что слишком стар, чтобы защищать новые идеи. А Лобачевский погибал без поддержки.

Больяи же, получив в 1848 году «Геометрические исследования», посчитал, что Гаусс выпустил мемуар под псевдонимом Лобачевский. Целью его жизни было превзойти этот труд. Это была агония разума – а Лобачевский даже не подозревал о существовании талантливого венгра.

За год до этого, зимой 1848 года, к Гауссу пришел студент. Его звали Бернард Риман. Но Гаусс оттолкнул его. Тогда Риман, сжав зубы, уехал в Берлин. Но мир тесен, и, защитив докторскую диссертацию, он решает стать профессором. Удивительно, но тему пробной лекции утверждает и принимает именно Гаусс.

Риман создал геометрию, где прямые замкнуты, где нет параллельных прямых, а сумма углов треугольника больше 180^о . Она похожа на геометрию сферы Гаусса.

Риман оказался хорошим учеником великого математика, и из нежеланного гостя стал единственным другом. Он умер в Италии, не закончив последний мемуар. На русском языке он появился только в 1893 году. Его название было: «О гипотезах, лежащих в основе геометрии».

Краткое описание геометрии Лобачевского.

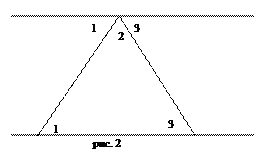
Иногда говорят, что в геометрии Лобачевского параллельные прямые пересекаются в бесконечности. Но это не совсем так. Есть только немного другое свойство параллельности: через одну точку вне прямой можно провести бесконечно много прямых, параллельных данной. Это видно на рисунке 1. Причем параллельность сохраняется только в сторону уменьшения расстояния между прямыми. Этот, казалось бы, простой факт, меняет всю геометрию. Как, например, в геометрии Евклида доказывается, что сумма углов треугольника равна 180^о ? Классическое доказательство приведено на рисунке 2. Используется свойство углов при накрест лежащих прямых, и выходит, что Ð1+Ð2+Ð3=180^о . Но так как в геометрии Лобачевского параллельность сохраняется только в одном направлении, то для нахождения суммы углов треугольника*, то нужно провести две прямые, параллельные данной в разные стороны. Что получается, видно на рисунке 3. Понятно, что теперь сумма углов треугольника меньше 180^о . Эта разница была названа Лобачевским дефектом треугольника.

Одними из важных объектов на плоскости Лобачевского являются пучки прямых. Но чтобы описать эти пучки, сначала надо уяснить, что в плоскости Лобачевского есть три типа расположения прямых: прямые или параллельны, или пересекаются, или являются расходящимися.
_______

* Здесь и далее подразумевается геометрия Лобачевского, если нет оговорки на геометрию Евклида.

Так вот, первый вид пучков образован прямыми, имеющими общую точку – центр пучка (рис. 4а). Пучок расходящихся прямых – это перпендикуляры к одной прямой – оси пучка (рис. 4б). Из этого определения выходит интересное и, казалось бы, абсурдное утверждение, что два перпендикуляра к одной прямой непараллельны, и отличие от геометрии Евклида.

И, наконец, пучок, образуемый прямыми, параллельными данной прямой в заданном направлении (рис. 4в).

Следующими объектами геометрии Лобачевского являются кривые. Для их построения Лобачевским было введено понятие соответственных точек. В пучке первого рода это точки на прямых, равноудаленные от центра (рис. 5а). В пучке второго рода это точки прямых, лежащие по одну сторону от оси и отстоящие от нее на одинаковые расстояния (рис. 5б). Наконец, в пучке третьего рода они расположены симметрично относительно биссектрисы полосы между двумя прямыми, на которых лежа эти точки (рис. 5в).