Реферат: Магнітне поле рухомого заряду

Оскільки рухомий електричний заряд в навколишньому просторі створює магнітне поле, то з сторони зовнішнього поля на цей заряд має діяти магнітна сила. Цю силу називають силою Лоренца .

Величину сили Лоренца визначимо, скориставшись силою Ампера

, (12.1.8)

де - сила, з якою зовнішнє магнітне поле діє на елемент провідника із струмом .

Замінюємо струм I на густину струму в провіднику j і його значення з електронної теорії

,

де n – концентрація носіїв струму в провіднику; q₀ – елементарний позитивний заряд; - середня швидкість направленого руху носіїв струму; S – переріз провідника.

У цьому випадку сила Ампера буде дорівнювати

, (12.1.9)

де - сила, з якою зовнішнє магнітне поле діє на магнітні поля всіх рухомих електричних зарядів, які є у виділеному елементі dl провідника.

Оцінимо число рухомих електричних зарядів у елементі струму Idl, яке в нашому випадку дорівнює

nSdl = dN .

Поділимо (12.1.9) на указане число електричних зарядів dN й одержимо

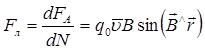, (12.1.10)

де - сила Лоренца – сила з якою зовнішнє магнітне поле діє на магнітне поле окремого електричного заряду; q_o - величина елементарного заряду; - середня швидкість направленого руху носіїв струму; B - індукція зовнішнього магнітного поля.

У векторній формі сила Лоренца записується так:

. (12.1.11)

Напрям вектора сили Лоренца визначається правилом лівої руки, аналогічно правилу лівої руки для напрямку сили Ампера.

При дії на рухому заряджену частинку електромагнітного поля сила Лоренца буде складатися із двох складників, електричної сили qE і магнітної сили , тобто

. (12.1.12)

Формула (12.1.12) є найбільш загальним виразом сили Лоренцо для малих швидкостей руху заряду.

Розглянемо рух зарядженої частинки в зовнішньому магнітному полі.

а) нехай заряджена частинка влітає перпендикулярно до напрямку силових ліній зовнішнього магнітного поля (рис.12.2).

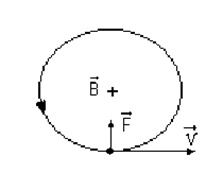
Рис.12.2

Сила Лоренца в цьому випадку виконує роль доцентрової сили, під дією якої заряджена частинка буде рухатися по коловій траєкторії. Рівняння руху зарядженої частинки запишеться

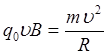, (12.1.13)

де ; m - маса частинки.

Визначимо радіус траєкторії обертання, а також період обертання, вважаючи, що