Реферат: Магнітне поле рухомого заряду

У цьому випадку радіус кривизни траєкторії й період обертання заряду будуть дорівнювати

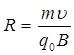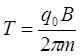; , (12.1.14)

де R - радіус кривизни траєкторії; m - маса частинки; - лінійна швидкість обертання; q_o - елементарний позитивний заряд; B - індукція магнітного поля.

б) у випадку руху зарядженої частинки паралельного напрямку силових ліній зовнішнього магнітного поля (рис.12.3) будемо мати.

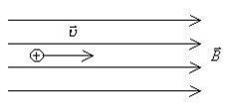
Рис. 12.3

Сила Лоренца в цьому випадку буде дорівнювати нулю, оскільки кут між векторами і дорівнює нулю. Зовнішнє магнітне поле не буде діяти на магнітне поле рухомої зарядженої частинки, якщо вона рухається паралельно силовим лініям зовнішнього магнітного поля.

в) якщо заряджена частинка попадає у зовнішнє магнітне поле під деяким кутом до напрямку силових ліній поля, то вона буде рухатись уздовж гвинтової траєкторії, як це показано на (рис.12.4).

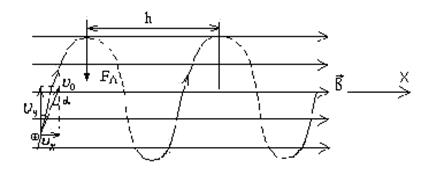
Рис.12.4

З рисунка видно, що

. (12.1.15)

Рівняння руху по коловій траєкторії буде мати вигляд

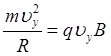, (12.1.16)

де ; R - радіус колової траєкторії.

Крок гвинтової лінії h , або шлях, який проходить заряджена частинка за один повний оберт у горизонтальному напрямі, можна розрахувати так:

, де . (12.1.17)

Період обертання визначають із рівняння руху (12.1.16), шляхом заміни лінійної швидкості на кутову, яку в свою чергу виражають через період обертання

.

2. Ефект Холла. Магнітогазодинамічний генератор та його використання

Розмістимо провідник зі струмом у перпендикулярне зовнішнє магнітне поле, як це показано на рис.12.5.

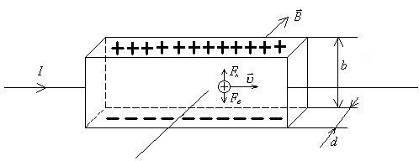
Рис. 12.5

Сила Лоренца зміщує рухомі електричні заряди, створюючи на гранях провідника різницю потенціалів, яку називають холлівською різницею потенціалів U_x .

Перерозподіл зарядів буде завершений, якщо сила Лоренца F_л стане дорівнювати електричній силі F_е , тобто

q B = qE = q , (12.2.1)

де b - ширина провідника; U_x – холлівська різниця потенціалів; q – елементарний позитивний заряд.

З (12.2.1) одержуємо

U_x = Bb.