Реферат: Магнитные наносистемы

где к – число контактирующих с кластером соседей.

Изменение свободной энергии Гиббса на стадии спекания составляет:

(4)

Для примера на рис.1 представлена зависимость для . Первый минимум в точке соответствует исходному состоянию маточной среды. Второй минимум в точке отвечает первому устойчивому состоянию – равновесному состоянию образовавшихся, но не контактирующих кластеров. Третий минимум соответствует системе кластеров имеющих к контактирующих соседних частиц, подвергаемых спеканию при условии . Соответственно первый максимум при представляет

собой потенциальный барьер нуклеации, второй - потенциальный барьер стадии спекания.

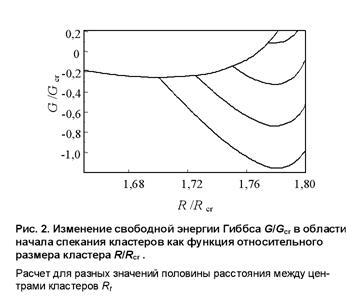
Рис.(2) демонстрирует вид потенциального барьера процесса спекания для к =6 и различных значений . В плотно заселенной кластерами системе, при , спекание

происходит без барьера. В менее плотно заселенной системе, при , процесс перехода к спеканию осуществляется через потенциальный барьер, а в еще менее плотно заселенной системе, при , спекание вообще не происходит.

На кривых дифференциального термического анализа и дифференциальной термической гравиметрии для процесса термического разложения оксалата железа на воздухе обнаруживаются два минимума: при и при . При выделяются ,, и начинает формироваться подвижная среда, в которой зарождаются и растут кластеры оксида железа. Второй минимум при , по-видимому связан с дальнейшим удалением из оксалата и , и началом спекания кластеров оксида железа.

Размер кластеров увеличивается с повышением от до . Его оценивали по величине удельной поверхности (по методу БЭТ), а также из данных рентгеноструктурного анализа атомно-силовой микроскопии и мессбауэровской спектроскопии.

Согласно зависимости на рис. (1), докритическая область размеров соответствует стадии флуктуационного зарождения кластеров. В области укрупнение кластеров сопровождается уменьшением свободной энергии, процесс протекает спонтанно и заканчивается образованием устойчивых кластеров размером , объединенных в систему слабовзаимодействующих неконтактирующих кластеров (система 1).

При дальнейшем повышении температуры создаются условия для массового образования контактов между кластерами () и начала спекания, в результате которого образуется система сильно взаимодействующих (спекшихся) кластеров размером (система 2). Значения и определяются условиями синтеза. Поэтому результат твердотельной топохимической реакции зависит от рабочей температуры продолжительности спекания и предыстории образца.

4.2 Магнитные свойства наносистемы оксидов железа

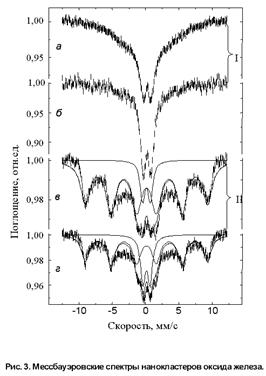
Изменение межкластерного взаимодействия от "слабого" к "сильному" приводит к изменению магнитных свойств наносистемы. Эти изменения исследовались методом мессбауэровской спектроскопии. Для системы 1 (изолированные кластеры) характерно явление суперпарамагнетизма, проявляющегося в виде тепловых флуктуаций магнитного момента кластера как целого, что приводит к размыванию магнитной сверхтонкой структуры спектра (рис. 3а,б). С момента образования системы 2 (взаимодействующие кластеры) появляется достаточно четко выраженная магнитная сверхтонкая структура с узким центральным парамагнитным дублетом (рис. 3в, г). Такой же эффект наблюдался ранее для нанокластеров ферригидрита, изолированных в порах полисорба, а также в кластерах и и в ядре железосодержащих белков ферритина и гемосидерина. Наблюдавшийся спектр мы объясняем как результат наличия в системе нанокластеров магнитного фазового перехода первого рода, при котором намагниченность или магнитный порядок изменяются скачком. Скачкообразный переход может наблюдаться при изменении температуры в некоторой критической точке , а также при изменении размера кластера, когда осуществляется переход через критическое значение радиуса . Скачкообразные переходы в наносистеме, обусловленные сильным межкластерным взаимодействием, давлением и деформацией, наиболее полно наблюдаются для системы 2, состоящей из крупных, спекшихся кластеров (20-50 нм) и . Отметим, что по данным рентгеноструктурного анализа обладает ромбоэдрической структурой, характерной для корунда, а - кубической структурой шпинели.

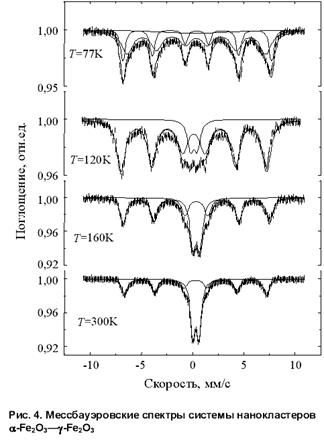
Мессбауэровские спектры наносистемы и (рис. 4) свидетельствуют о наличии в ней скачкообразных магнитных переходов между магнитоупорядоченным состоянием с характерной сверхтонкой структурой и парамагнитным состоянием, к которому отнесен центральный дублет.

Эти магнитные переходы происходят при температурах , которые ниже критических температур , характерных для массивных образцов и (856 и 965 К соответственно). Понижение критической температуры (по сравнению с ) не может быть следствием суперпарамагнетизма из-за больших размеров кластеров, составляющих систему. Расчет времени релаксации по формуле, используемой для описания релаксации в суперпарамагнитных системах

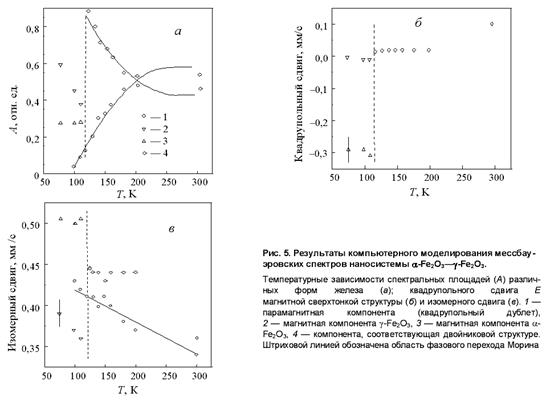
где ; К - константа магнитной анизотропии кластера; V – объем кластера, дает значения на несколько порядков большие времени измерения, равному . В результате магнитная индукция исчезает скачкообразно, что обусловлено трансформацией магнитной сверхтонкой структуры в парамагнитный дублет (рис. 5а).

Наличие в наносистеме и фазового перехода первого рода связано с "сильным" межкластерным взаимодействием. При спекании кластеров кардинально меняется кривизна их поверхности, которая, как показали оценки, определяет возможность существования скачкообразного магнитного перехода [2].

Кроме магнитного фазового перехода первого рода в этой системе наблюдаются еще два фазовых перехода: слабый ферромагнетик – антиферромагнетик и коллективный магнитный фазовый переход с образованием двойниковых наноструктур. Слабый ферромагнетизм (неколлинеарный антиферромагнетизм) возникает при повышении температуры, как следствие нестабильности скомпенсированного антиферромагнетизма. Для массивного образца существует магнитный фазовый переход при , известный как переход Морина, когда в структуре скачком изменяется тип магнитного упорядочения. При имеет место коллинеарный антиферромагнетизм, а при - неколлинеарный антиферромагнетизм (слабый ферромагнетизм). Этот переход сопровождается поворотом спинов на .

В мессбауэровских спектрах фазовый переход "коллинеарность – неколлинеарность магнитных моментов" с поворотом направления спинов относительно направления градиента кристаллического поля определяется по изменению знака и величины квадрупольного расщепления спектра , обладающего магнитной сверхтонкой структурой. Так, для массивного образца высокотемпературной фазе соответствует мм/с, а низкотемпературной мм/с. Особенности этого фазового перехода в наносистеме и прослеживаются из рис. 5б. Низкотемпературная фаза ( мм/с), обладающая при коллинеарным антиферромагнетизмом, при переходит в состояние неколлинеарного антиферромагнетизма с мм/с (высокотемпературная фаза). Таким образом температура перехода Морина наносистемы по сравнению с поведением массивного материала понижается до 120 К , причем высокотемпературная фаза имеет меньшее значение , чем характерное для массивного материала. С уменьшением размера кластера обменная энергия уменьшается (понижается ) и вероятность существования неколлинеарного антиферромагнетизма возрастает.<