Реферат: Малошумящие однозеркальные параболические антенны

l - длина волны излучаемого (принимаемого) антенной радиосигнала;

R – радиус раскрыва зеркала (рис. 1)

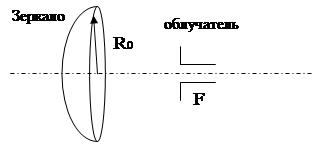
Рис.1. Зеркальная параболическая антенна.

Однако, добиться равномерного возбуждения раскрыва практически не удается. Известно, что коэффициент направленного действия зеркальной антенны имеет наибольшую величину в том случае, если амплитуда возбуждающего поля на краю раскрыва составляет не менее одной трети от амплитуды поля в центре раскрыва.

Неравномерное возбуждение раскрыва зеркала приводит к некоторому расширению главного лепестка диаграммы направленности, так как уменьшается эффективная площадь раскрыва. Кроме этого, необходимо иметь в виду, что чаще всего диаграммы направленности зеркальных антенн не обладают осевой симметрией, (большинство излучателей формируют осенесимметричные диаграммы направленности), т.е. ширина главного лепестка в плоскостях Е и Н различна. В большинстве практических случаев это влечет за собой следующее изменение выражения (1):

2q≈1.2 (2)

2q≈1.3 (3)

где 2q,2q - ширина диаграммы направленности соответственно Н и Е плоскостях.

Тогда R для Н плоскости:

(м)

R для Е плоскости:

(м)

В связи с тем, что в задании на курсовую работу имеются данные о ширине диаграммы направленности в обеих плоскостях, из выражений (2) и (3) определяем диаметр раскрыва d= 2R, при, чем, из полученных двух значений диаметра выбираем наибольшее, т.е.:

d=2*0.315(м), следовательно: =0.63(м)

1.2 Определение угла раскрыва и фокусного расстояния зеркальной антенны.

В зависимости от размещения облучателя относительно зеркала можно получить, то или иное значение КНД. При определенном оптимальном отношении R/f КНД наибольший. Это объясняется тем, что количество теряемой энергии зависит от формы диаграммы направленности облучателя и отношения R/f. При уменьшении отношения R/f от оптимального КНД уменьшается, т.к. увеличивается часть энергии, проходящей мимо зеркала. С другой стороны, увеличение этого отношения также приводит к уменьшению КНД в связи с более сильным отклонением закона распределения возбуждения от равномерного; оптимальное значение R/f определяется по апроксимированной нормированной диаграмме направленности облучателя (апроксимация функцией вида F()= cos (), где n определяет степень вытянутости диаграммы направленности облучателя).Для рупорных облучателей значения приводим в таблице ниже:

N	R/f	ν
6	0.8…1	0.81

F()= cos ()=cos

Расчет апроксимации диаграммы направленности облучателя приведен в приложении.

В зависимости от значения n определяем оптимальную величину отношения R/f. Более точное значение R/f определяем из графиков зависимости КИП ν параболоида от угла раскрыва ψ, при различных n.

Из велличины отношения R/f с учетом расчетного R определяем значение f:

f= R/(0.8…1.0)=0.315/0.9=0.35 (м)

Угол ψ может быть рассчитан на основе следующего соотношения:

ψ= 2 arctg= 2arctg=2 arctg(0.45)=48

2. РАСЧЕТ ГЕОМЕТРИЧЕСКИХ И ЭЛЕКТРОДИНАМИЧЕСКИХ ХАРАКТЕРРИСТИК ОБЛУЧАТЕЛЕЙ.

Расчет сводится к определению геометрических размеров облучателя, при которых уменьшение амплитуды поля на краю раскрыва зеркала происходит до одной трети амплитуды поля в центре раскрыва и диаграммы направленности облучателя.

Диаграмму направленности конического рупора рис(2) определяем как для идеальной круглой излучающей поверхности радиусом a:

F()=,

где J ( sin) – цилиндрическая функция Бесселя первого рода,