Реферат: Математическая модель метода главных компонент

Программа для реализации метода главных компонент была написана на языке Turbo Pascal 7.0 . Все вычисления выполнены в последовательности, представленной на рисунке 1.1. Обозначения программных переменных и массивов по возможности соответствуют изложенным выше. Программа является в достаточной степени универсальной, т.к. приспособлена для обработки массивов данных любой размерности (их размер ограничен только объемом доступной памяти). Однако в программе не предусмотрен ввод данных с клавиатуры. Размерность массивов задана константами, а массив исходных данных инициализируется также в теле программы. При необходимости ввода других данных можно легко скорректировать исходный текст программы.

Отдельной процедурой в программе описан вывод на экран матрицы m*m. В программе часто приходится проделывать эту операцию, поэтому она оформлена как процедура out.

Первой процедурой является центрирование и нормирование исходных данных. Оно выполняется в соответствии с описанными выше формулами.

Далее запрограммировано нахождение коэффициентов характеристического уравнения для корреляционной матрицы R . Оно производится в соответствии с рекуррентными соотношениями Фаддеева, т.е по следу матриц, производных из R , по формулам:

A_i-1 =AB_i-2 ; P_i-1 =1/(m-1)t_r A_i-1 ; B_i-1 =A_i-1 -P_i-1 E ; i=1,2..m . (2.1)

После вычисления рекуррентных соотношений находится характеристический полином:

P_m (λ)= λ^m - P₁ λ^m-1 - P₂ λ^m-2 -…- P_m . (2.2)

Известно, что при m > 4 (2.2) не имеет общего решения. Однако мы знаем, что это уравнение имеет все вещественные корни, и что их число равно m . Для их нахождения используется итерационный метод Ньютона, поскольку исследуемая функция – полином и нет затруднений в вычислении ее производной. Итерационная формула Ньютона для i -й точки имеет вид:

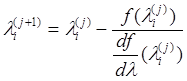, (2.3)

где j – номер итерации.

Далее в соответствии с (1.1) находим собственные векторы матрицы R . Для решения систем уравнений применялся метод Гаусса. Однако предварительно необходимо было исключить одно неизвестное. Для этого переменным u_mj были присвоены единичные значения, последний столбец перенесен в правую часть с обратным знаком, а последнее уравнение исключено из рассмотрения.

После получения матрицы собственных векторов U было проведено ее нормирование, в результате чего была получена матрица нормированных собственных векторов V .

Затем вычисляется матрица факторного отбражения A в соответствии с правилами умножения матриц.

Далее находится матрица, обратная к A , методом m -кратного пересчета элементов [3,с.358] по рекуррентным формулам:

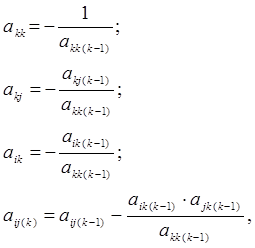
где k – номер итерации, k=1..m . На заключительном этапе A^-1 = -A_(k) .

После нахождения матрицы, обратной A , находим матрицу F – матрицу факторного отображения и выводим ее на экран в транспонированном виде в соответствии с (1.2). На этом расчеты по методу главных компонент завершены.

ЗАКЛЮЧЕНИЕ

В данной курсовой работе была построена математическая модель и программная реализация метода главных компонент. Следует отметить, что в работе не была рассмотрена методика отсева несущественных факторов, и поэтому результирующая модель, выдаваемая программой на экран, содержит число компонент, равное числу исходных элементарных признаков m . К достоинствам разработанной программы можно отнести то, что она может работать с массивами исходных данных достаточно большой размерности.

ЛИТЕРАТУРА

1 Сошникова Л.А., Тамашевич В.Н., Уебе Г., Шебер М. Многомерный статистический анализ в экономике: Учеб. Пособие для вузов/Под ред. проф. Тамашевича. – М.: ЮНИТИ-ДАНА, 1999. –598с.

2 А. Епанешников, В. Епанешников. Программирование в среде Turbo Pascal 7.0. –3-е изд., стер. –М.: “ДИАЛОГ-МИФИ”, 1997. –288с.

3 Жуков Л.А., Стратан И.П. Установившиеся режимы сложных электрических сетей и систем: Методы расчетов. –М.: Энергия, 1979. – 416 с.

ПРИЛОЖЕНИЕ А

Текст программы метода главных компонент

Program gl_komp;

const

m=3;{число признаков}

n=4;{число объектов}

type

matrix=array[1..m,1..m]of real;

var

x,z:array[1..n,1..m]of real;