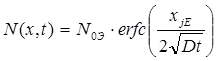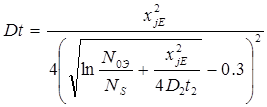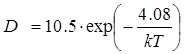Реферат: Математическое моделирование технологического процесса изготовления ТТЛ-инвертора

1.3 Распределение примесей в эмиттере

Эмиттерную диффузию ведут в одну стадию и распределение примеси описывается erfc-функцией:

(5)

где - концентрация предельной растворимости мышьяка в кремнии при заданной температуре (1100°С);

- глубина залегания эмиттерного p-n перехода.

Диффузия мышьяка идёт в неоднородно легированную базовую область, поэтому расчётная формула усложняется:

(6)

где при 1100°С;

.

Подставив эти значения в выражение 6 получим: .

Подставляя это значение в выражение 5 получим распределение мышьяка в эмиттерной области после диффузии. График распределения представлен на рисунке 1.

1.4 Расчет режимов эмиттерной диффузии

Найдём, по аналогии с базовой диффузией, для эмиттерной время и температуру процесса. В данном случае температура процесса задана (1100°С) и необходимо найти только время диффузии. Для этого необходимо сначала определить коэффициент диффузии, который находится из выражения 4. Постоянная диффузии D₀ энергия активации для фосфора равны 10,5 и 4,08 соответственно. Тогда получаем:

Решив это уравнение получим:

;

t=98мин 33сек.

Так как эмиттерная диффузия проходит при высоких температурах, то она оказывает влияние на диффузию бора в базовой области. Необходимо учитывать это влияние. Учесть эмиттерную диффузию при базовой можно по следующей формуле:

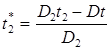. (7)

Таким образом время разгонки при базовой диффузии с учётом влияния эмиттерной диффузии t₂ =53мин 44сек.. В таблице 2 представлены все основные параметры диффузионных процессов.

Таблица 2 – Параметры диффузионных процессов

Параметр	Эмиттерная диффузия	Базовая диффузия
Загонка	Разгонка
Dt,
D,
t	98мин 33с	15мин 48с	53мин 44с*

* - время разгонки, представленное в таблице, уже с учётом эмиттерной диффузии

Совмещённое распределение примесей определяется выражением:

(8)

где , , - концентрации эмиттерной, базовой и коллекторной областей соответственно, в данной точке.

График совмещённого распределения примесей представлен на рисунке 2.

Таблица 3-Распределение примесей в транзисторной структуре

Глубина залегания примеси	Распределение примеси в эмиттере	Распределение примеси в базе	Суммарное распределение
x, см	N(x), см -3	N(x), см -3	N(x), см -3
0	1,6ּ10 21	2ּ10 18	1,59ּ10 21
4ּ10 –6	1,17ּ10 21	1,98ּ10 18	1,17ּ10 21
8ּ10 –6	7,81ּ10 20	1,94ּ10 18	7,79ּ10 20
1,2ּ10 –5	4,83ּ10 20	1,86ּ10 18	4,81ּ10 20
2,8ּ10 –5	2,59ּ10 19	1,36ּ10 18	2,45ּ10 19
3,2ּ10 –5	9,13ּ10 18	1,21ּ10 18	7,98ּ10 18
3,6ּ10 –5	3,13ּ10 18	1,06ּ10 18	2,05ּ10 18
4,8ּ10 –5	6,47ּ10 17	6,32ּ10 17
5,6ּ10 -5	4,31ּ10 17	4,16ּ10 17
6,4ּ10 –5	2,69ּ10 17	2,54ּ10 17
7,2ּ10 –5	1,58ּ10 17	1,43ּ10 17
8ּ10 –5	8,73ּ10 16	7,23ּ10 16
8,8ּ10 –5	4,52ּ10 16	3,02ּ10 16
9,6ּ10 –5	2,02ּ10 16	7,02ּ10 15
1,05ּ10 –4	9,08ּ10 15	5,91ּ10 15
1,1ּ10 –4	5,37ּ1015	9,62ּ10 15
1,15ּ10 –4	3,09ּ10 15	1,19ּ10 16
1,2ּ10 –4	1,74ּ10 15	1,33ּ10 16
1,3ּ10 –4	5,13ּ10 14	1,44ּ10 16
1,4ּ10 -4	1,36ּ10 14	1,48ּ10 16
1,5ּ10 –4	3,31ּ10 13	1,49ּ10 16

1- Распределение мышьяка в эмиттерной области после диффузии;

2- Распределение бора в базовой области после диффукзии;

3- Концентрация примеси в коллекторе

Рисунок 1-Профиль распределения примесей в эмиттере и базе

Рисунок 2- Суммарное распределение примесей эмиттера и базы

2 Расчет слоевых сопротивлений биполярного транзистора