Реферат: Медианы треугольника

АВ'=В'С.

Второе доказательство(8 класс).

Рассмотрим гомотетию с центром М и коэффициентом -1/2. Точка А переходит при этой гомотетии в . Пусть В переходит в В' (рис. 2). Тогда = - АВ. С другой стороны, средняя линия получается из стороны ВА при гомотетии с центром С и коэффициентом 1/2; таким образом:

=

Итак, , следовательно, В'=. Таким образом, треугольники ABC и гомотетичны, причем центр гомотетии лежит в точке М. По определению гомотетии, точки В, М и В' = лежат на одной прямой.

Третье доказательство(9 класс).

Рассмотрим треугольники MAC и МС (рис. 3). Их высоты, опущенные из вершины С, совпадают, а длины противолежащих этой вершине сторон относятся как 2:1, поэтому , где S обозначает площадь. Аналогично, . Но . Следовательно,

. Таким образом, треугольники МАВ, МВС и МСА равновелики. Пусть В' - точка пересечения прямых ВМ и АС. Докажем, что АВ' = В'С. С одной стороны,

С другой стороны,

.

Пользуясь теоремой

,

отсюда получаем

.

Четвертое доказательство (9 класс).

ВМ= ВС + СА+АМ=ВС + СА+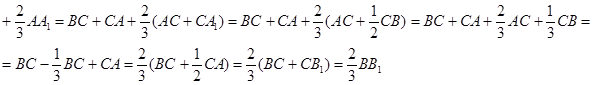

Следовательно, точка М лежит на медиане .

Пятое доказательство (9 класс).

Опять рассмотрим точку В' пересечения прямых ВМ и АС (рис. 3). Применяя теорему синусов сначала к треугольникам АВ'В и СВ'В, а затем - к треугольникам АВМ и ВМ и учитывая, что sinAB ' B = sinCB ' B , sinAMB = = sinMB , BC=2Bи МА = 2M, получим

.

Шестое доказательство(10 класс).

Проведем через точки А и В плоскость а, не содержащую С, и построим в этой плоскости правильный треугольник ABC (рис. 5). Из общих свойств параллельной проекции следует, что параллельная проекция вдоль прямой С переводит треугольникАВС в треугольник АВ, причем медианы треугольника ABC проектируются в медианы треугольника AB . Но в правильном треугольнике медианы являются и биссектрисами, а следовательно, пересекаются в одной точке. Легко доказать также (докажите!), что для треугольника AB справедливы равенства (1).

Отсюда вытекает, что наша теорема верна и для треугольника АВС.

Упомянем еще одно, быть может, самое простое и естественное доказательство теоремы о медианах: если поместить в вершины треугольника равные массы и поочередно группировать их парами, мы получим, что центр всех трех масс лежит на каждой из медиан. Центр системы равных масс, помещенных в некоторые точки, называется центроидом этого набора точек, поэтому и точку пересечения медиан треугольника часто называют его центроидом.

Заключение

Исходя из проделанной работы можно сделать следующие выводы:

1. Одну теорему можно доказать разными способами. Это гораздо полезнее. Ведь ее можно изучить с разных сторон, используя различные методы и темы курса 8-10 классов.