Реферат: Механический и магнитный моменты атома

Рассмотрим закономерности определения квантового числа механического момента атома, в частности, для случая LS – связи.

Квантовые орбитальные числа электронов l – целые, следовательно, квантовое орбитальное число атома L также целое число.

Квантовое спиновое число электрона s = , поэтому квантовое спиновое число атома S либо целое (если в атоме четное число электронов Z), либо полуцелое (Z – нечетное).

Квантовое число J результирующего механического момента атома по аналогии с полным квантовым числом электрона j определяется как

J = |L – S|, |L – S -1| …0, … (L + S - 2), (L+S – 1), (L+S)

или

J = 0, ±, ± 1 … ± |L±S|, включая полуцелые.

Существуют правила отбора квантовых чисел атома:

ΔL = ± 1,ΔS = 0,ΔJ = 0, ± 1

Магнитный момент атома

Как уже говорилось ранее, орбитальный и магнитный моменты электрона связаны гиромагнитным отношением: .

Экспериментально было доказано, что для механического и магнитного орбитальных моментов атома выполняется аналогичное соотношение .

Подставляя , где L – квантовое орбитальное число атома, получаем

, (*)

Так же, как и для электрона, для атома спиновое гиромагнитное отношение в два раза больше гиромагнитного отношения для орбитальных моментов , и соотношение между спиновыми моментами атомами аналогично полученному ранее для электрона

():,(**)

так как , где S – квантовое спиновое число атома.

Полный момент импульса атома

Полный магнитный момент атома связан с полным механическим моментом следующим соотношением:

,

где 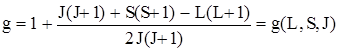– множитель (или фактор) Ланде, который вводится для того, чтобы учесть различие в два раза гиромагнитных отношений орбитальных и спиновых моментов или так называемый удвоенный магнетизм спина (сравни выражения * и **). Множитель Ланде может равняться нулю и быть меньше 1, так как представляет собой комбинацию квантовых чисел атома.

Атом в магнитном поле

Как уже говорилось, во внешнем магнитном поле векторы и электрона в атоме прецессируют с угловой скоростью 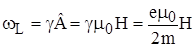. При квантово-механическом рассмотрении влияния магнитного поля на атомы выявлено, что по аналогии с прецессией электронных моментов имеет место прецессия векторов механического и магнитного момента атома – и под определенным углом к направлению вектора магнитной индукции . Однако проекции вектора на направление магнитного поля – могут принимать лишь значения, определяемые полным магнитным квантовым числом М:. Полное магнитное число М может принимать (2J+1) значений:М = 0, ± 1, ± 2…± J.

Таким образом, атом, обладающий магнитным моментом , приобретает в магнитном поле дополнительную энергию, которая определяется фактором Ланде данного атома. Каждый энергетический уровень атома расщепляется на (2J+1) равноотстоящих уровней, что приводит к образованию большого числа спектральных линий. Однако необходимо учитывать правило отбора для полного магнитного числа М, аналогичное правилу отбора для магнитного квантового числа электрона m:ΔМ = 0, ± 1.