Реферат: Механічна енергія

, (3.1.7)

то формулу для роботи можна переписати у вигляді

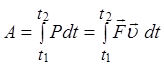, (3.1.8)

тобто роботу можна виразити через інтеграл від потужності й часу, а також через скалярний добуток вектора сили й вектора швидкості. В останньому випадку сила, перпендикулярна до вектора швидкості, роботи не виконує.

З урахуванням другого закону Ньютона 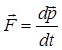вираз для механічної роботи набуде вигляду:

. (3.1.9)

Оскільки , а , то

. (3.1.10)

Якщо швидкість матеріальної точки в процесі руху змінюється від 1 до 2, то робота, яка виконується у цьому випадку, буде дорівнювати

. (3.1.11)

Скалярна величина називається кінетичною енергією. Таким чином ми довели, що робота сили по переміщенню матеріальної точки дорівнює зміні її кінетичної енергії.

Слід також пам’ятати, що в цьому прикладі ми мали справу з повною силою, діючою на точку. Так, у випадку переміщення саней уздовж не дуже гладенької дороги, посипаної піском, виконується робота, відмінна від нуля. Приросту кінетичної енергії тут не буде. Вся справа в тому, що сила опору руху саней має протилежний напрям. Робота цієї сили має від’ємний знак. Сила тертя теж виконує роботу, але від’ємну. А в результаті повна сила і повна робота виявляються рівними нулю.

2. Консервативні й неконсервативні сили. Потенціальна енергія. Зв’язок роботи й потенціальної енергії

Всі сили, які зустрічаються в механіці макроскопічних тіл, прийнято поділяти на консервативні й неконсервативні.

До консервативних сил відносяться такі сили, робота яких не залежить від форми шляху між двома точками 1 і 2 (рис.3.2).

A1,2(a) =A1,2(b) =A1,2(c)

Рис. 3.2.

Прикладом консервативних сил є сила тяжіння Землі. Робота сили тяжіння при перенесенні матеріальної точки із положення 1 в положення 2, уздовж прямолінійного відрізку (рис.3.3) дорівнює:

Рис.3.3.

, (3.2.1)

де h1 і h2 - висоти, на яких перебувала матеріальна точка на початку і в кінці шляху. Вираз роботи (3.2.1) справедливий для переміщення з точки 1 в точку 2 на будь-якому шляху.

Ще одним прикладом консервативних сил є так звані центральні сили. Прикладом центральних сил можуть бути гравітаційні сили планет і зірок, кулонівські сили точкових зарядів обох знаків, ядерні сили (на дуже малих відстанях) тощо.

Покажемо, що робота центральних сил не залежить від форми шляху. Знайдемо роботу сили гравітаційного притягання двох точкових мас m і М у випадку переміщення точкової маси m з точки 1 в точку 2 в гравітаційному полі точкової маси М (рис.3.4).

Рис.3.4.

. (3.2.2)

В даних перетвореннях . Тому

. (3.2.3)