Реферат: Механизмы качающегося конвейера
![]()
![]()
Определяем скорости точки D. Для определения скоростей точки D, составляем уравнение:
![]()
где: VB -известно по направлению и по значению; VDB - известно по направлению, но неизвестно по значению; VD - известно по направлению, но неизвестно по значению. На плане скоростей из точки b проводим прямую, перпендикулярно звену BD. Из полюса скоростей Pv из проводим горизонтальную прямую (т.к. ползун 5, движется поступательно). На пересечении этих прямых обозначаем точку d . Вектор PV D - графический аналог скорости VD и вектор bd - графический аналог скорости VDB .
Находим действительные значения VD и VDB :
![]()
![]()
Определяем скорости точек центров масс звеньев. По условия, центры масс (на схеме механизма обозначены как S2 , S3 , S4 , S5 ) находятся посередине звеньев ![]() .
.
Определяем скорость точки S2 . Из полюса скоростей PV , проведем прямую через середину отрезка ab и обозначим точку S2 . Вектор Pv S2 , будет графическим аналогом скорости VS2 .
Определяем действительное значение скорости VS2 :
![]()
Определяем скорость точки S3 . Скорость точки S3 будет находиться на середине отрезка PV b. Обозначим точку S3 . Вектор Pv S3 , будет графическим аналогом скорости VS3 .
Определяем действительное значение скорости VS3 :
![]()
Определяем скорость точки S4 . Из полюса скоростей PV , проведем прямую через середину отрезка bd и обозначим точку S4 . Вектор Pv S4 , будет графическим аналогом скорости VS4 .
Определяем действительное значение скорости VS4 :
![]()
Определяем скорость точки S5 . Так как точка S5 совпадает с точкой D, то и скорости VD и VS5 будут равны. Следовательно, скорость VS5 =0,74 м/с.
Определяем угловые скорости w звеньев механизма для данного положения.
Звено 1.
По условию w1 =const, следовательно у звена 1 угловая скорость во всех положениях будет постоянной:
![]()
Звено 2.
Угловая скорость звена 2 определяется по формуле:
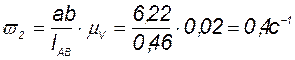
где: ab – длина отрезка на плане скоростей, мм ; lAB – действительная длина звена 2, м;
mV – масштабный коэффициент плана скоростей.
Звено 3.