Реферат: Методи обробки ЕЕГ

– відліки за часом.

Отримані спектри наведені на рис. 3, де на графіках показані спектри вихідної ЕЕГ (суцільна), згладженої за допомогою ФК (пунктир). Як видно, видалення шуму фактично являє собою фільтрацію високочастотних складових процесу.

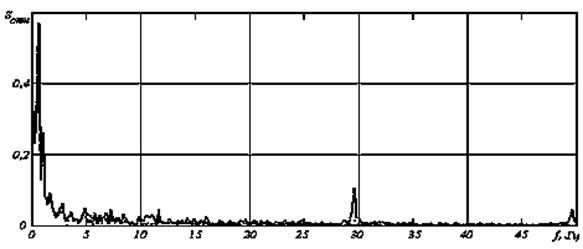
Рисунок 3 – Спектри вихідної ЕЕГ (суцільна), згладженої за допомогою ФК (пунктир)

3. Фазочастотний метод аналізу миттєвих характеристик ЕЕГ

Спектрально-кореляційні методи дозволяють визначити домінування визначених частотних складових на даному відрізку ЕЕГ і за цими даними знайти, зокрема, зону розташування патологічного вогнища. Однак вони не дають можливості детально простежити і чисельно охарактеризувати динаміку зміни структури ЕЕГ у часі, зміну і тривалість ритмів. Фазочастотний метод заснований на представленні випадкового процесу у вигляді . При цьому випадковий процес розглядається як гармонійне коливання, модульоване за амплітудою і фазою випадковими функціями і . Обчислення цих функцій дозволяє спостерігати зміну амплітуди і фази ЕЕГ у часі, а також досліджувати зміну в часі миттєвої і середньої частот коливань, якщо підходити до поняття частоти як похідної фази коливального процесу. Такий метод аналізу дозволяє чисельно охарактеризувати тривалість і частоту зміни окремих ритмів.

Можливість представлення випадкового процесу у вигляді гармонійного коливання, промодульованого випадково за амплітудою і фазою, досить теоретично обґрунтована. Представимо випадковий процес у формі

. (5)

Зв'язок між , і можна встановити за допомогою інтегральних перетворень Гільберта

, ,

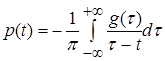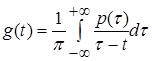причому при беруться головні (у понятті Коші) значення інтегралу. Функція називається спряженим процесом стосовно .

Огинаюча процесу і фаза визначаються так:

, .

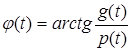Представлення випадкового процесу у вигляді (5) легко інтерпретувати у випадку вузькосмугових процесів. У цьому випадку велику наочність набуває поняття огинаючої, в яку вписується гармонійне чи майже гармонійне коливання. Крім того, можна визначити миттєву частоту процесу за допомогою співвідношення

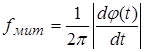. (6)

ЕЕГ є широкосмуговим процесом, і в цьому випадку поняття огинаючої не має чіткого фізичного змісту. Середню чи поточну частоту коливального процесу зазвичай визначають за числом періодів в одиницю часу, не користуючись похідною фази. Цими обставинами можна пояснити той факт, що аналіз широкосмугових процесів за допомогою виразу (6) на практиці зазвичай не використовується. Водночас аналіз функції дозволяє одержати деяку додаткову інформацію про стабільність частотних характеристик, час стаціонарності і характер перехідних режимів у коливальному процесі.

Введення для широкосмугових процесів поняття поточної частоти шляхом усереднення фазової кривої на деякому інтервалі часу дає можливість охарактеризувати тривалість і частоту зміни характерних коливань (ритмів у випадку ЕЕГ) у досліджуваному процесі.

Для ілюстрації можливостей методу фазочастотного аналізу на рис. 4 показані відрізки штучно складених реалізацій і відповідні цим реалізаціям фазові і частотні криві. Реалізація, зображена на рис. 4, складена з відрізків синусоїд з різними амплітудами і частотами. З рисунка видно, що фазові залежності в межах синусоїдальних відрізків являють собою прямі лінії, що відповідають коливанням з постійною частотою. Стрибки фаз у коливальному процесі знаходять чітке відображення на фазовій кривій. Відрізкам синусоїд з однаковою частотою, але різними амплітудами відповідає той самий нахил фазової кривої, тобто та сама частота коливань.

Реалізація, показана на рис. 5, отримана шляхом довільного перекручування (модуляції) форми синусоїди накладенням більш високочастотного коливання невеликої амплітуди. Як видно з фазової кривої, наявність високочастотних низькоамплітудних коливань, що модулюють, приводить до перекручування форми фазової кривої та її відхилення від прямої лінії. Однак частота, отримана шляхом згладжування цієї кривої, дорівнює частоті неспотвореної синусоїди. Отже, на фазовій кривій можна виділити частоту високоамплітудного коливання.

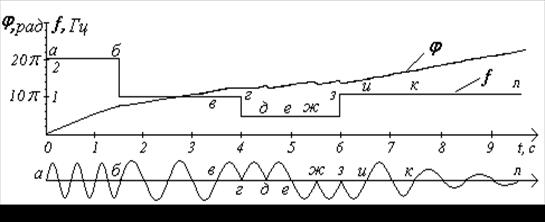
Рисунок 4 – Реалізація, складена з відрізків синусоїд з різними амплітудами і частотами та її фазова й частотні криві

Штучна реалізація, показана на рис. 6, може служити прикладом випадкового слабкокорельованого широкосмугового процесу (на цьому рисунку і – амплітудний спектр і автокореляційна функція відповідно). Форма фазової кривої в цьому випадку складна, визначити по ній частотні характеристики процесу можна двома способами. По-перше, згладивши криву в межах відрізків часу , протягом яких відрізки кривої добре апроксимуються відрізками прямої, можна одержати значення поточної частоти процесу.

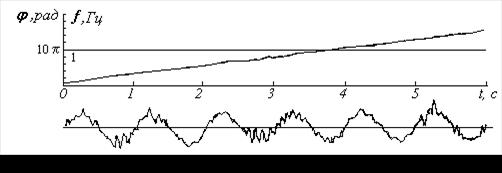
Рисунок 5 – Реалізація, отримана шляхом довільного перетворювання (модуляції) форми синусоїди накладенням більш високочастотного коливання невеликої амплітуди та її фазова й частотні криві

На рис. 6 показана частотна крива, що відповідає такому усередненню.
З урахуванням висновку, зробленого під час розгляду рис. 5, можна сказати, що поточна частота, яка відповідає високоамплітудній низькочастотній складовій спектра коливання за час , змінюється в невеликих межах.

Частотна крива на рис. 6 характеризує зміну в часі поточної частоти процесу і горизонтальні площадки на частотній кривій визначаються відрізками часу, протягом яких поточна частота практично не змінюється. В інших можна усереднити усю фазову криву, з'єднавши прямою крайні точки цієї кривої.

У цьому випадку визначення повного приросту фази за весь аналізований відрізок часу дозволяє знайти деяку середню частоту процесу.

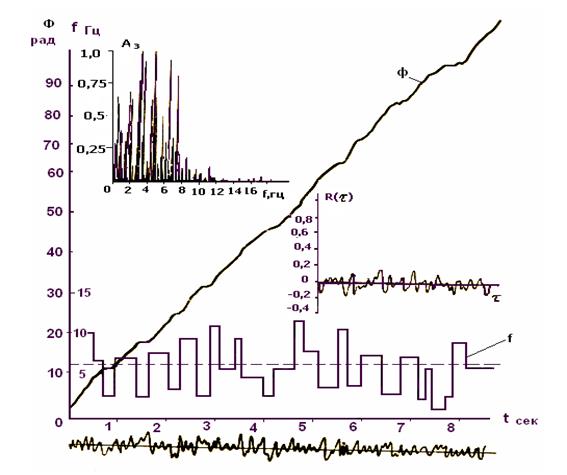
Рисунок 6 – Реалізація ЕЕГ, спектр і функція автокореляції