Реферат: Методы анализа транзисторных усилительных каскадов
Так как сопротивлениями емкостей С Э , С Ф , С Р можно пренебречь, то резисторы R К и R Н оказываются включенными по переменной составляющей параллельно и на них создается падение напряжения
. (6.61)
В свою очередь
.
Теперь формулу 6.61 можно переписать в следующем виде:
.
Выходное напряжение оказывается в
(6.62)
раз больше входного. В этом и состоит эффект усиления. Также необходимо подчеркнуть, что выходное напряжение оказывается сдвинуто по фазе относительно входного напряжения на 180°, на что указывает знак "минус" в формулах.
Анализ свойств различных схемных построений осуществляют на основе соотношений и положений теории четырехполюсника и эквивалентных схем каскадов (Рис.6.13).
Рис.6.13. Эквивалентная схема каскада
При этом УЭ рассматривают в виде четырехполюсника, к выходным клеммам которого 2-2` подключена нагрузка R Н , а к входным 1-1` - источник сигнала с ЭДС Е С и сопротивлением Z С , а для анализа используют известные методы расчета электрических цепей.
Принципы приведенных расчётов могут быть распространены и на случаи, когда условия малосигнальности не выполняются (если отклонения DI ВЫХ , DU ВЫХ превышают 20 - 30% от I ВЫХ , U ВЫХ в исходной РТ). Необходимо использовать усредненные значения h- параметров, под которыми понимают полусуммы их значений, отвечающих крайним отклонениям выходных токов и напряжений, наблюдаемых в процессе усиления сигналов.
Вышеприведенные рассуждения справедливы для случая, когда сопротивлениями разделительных и блокировочных конденсаторов можно пренебречь в силу их малых значений (в эквивалентных схемах замещения эти конденсаторы заменяются короткими замыканиями). На низких частотах выполнить условия пренебрежимо малого значения емкостного сопротивления не удается, в результате чего в усилительном каскаде возникают низкочастотные искажения. Для снижения этих искажений требуется увеличение емкостей конденсаторов С Р , С Б , что не всегда выполнимо из конструктивных или экономических соображений. Поэтому номиналы С Р , С Б выбирают исходя из предельно допустимых частотных искажений.
Эквивалентная схема сигнальной цепи, содержащей разделительный конденсатор, приведена на рисунке 6.14, при этом рисунок 6.14, а соответствует случаю, когда сигнальные изменения представлены с помощью генератора тока, а рисунок 6.14, б - с помощью генератора ЭДС.
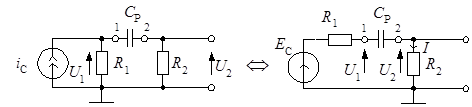
а б
Рис.6.14. Эквивалентные схемы сигнальной цепи с конденсатором С Р
Оба представления взаимно эквивалентны. Рассмотрим передаточные свойства этой цепи на участке 1 - 2.
На средних частотах, когда сопротивление С Р пренебрежимо мало, коэффициент передачи частотно независим и равен
(6.63)
По мере понижения частоты сопротивление конденсатора растет, и общее выходное напряжение цепи падает. Коэффициент передачи разделительной цепи для низких частот будет равен
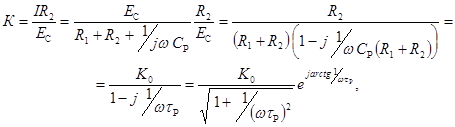(6.64)
где 
- постоянная времени разделительной цепи.
Анализ выражения (6.64) показывает, что влияние разделительной цепи на низких частотах сказывается уменьшением модуля коэффициента передачи (график на Рис.6.15) и появлением дополнительного фазового сдвига (Рис.6.16).
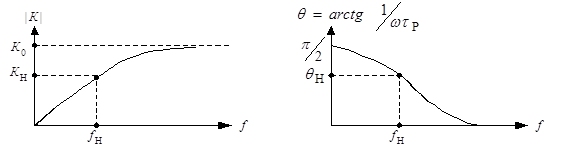
Рис.6.15. График |K | Рис.6.16. График q ( w)
Если задаваться некоторой нижней границей частотного диапазона w Н , можно определить коэффициент частотных искажений МН для заданной схемы: