Реферат: Методы дискриминантного анализа
-затраты на сырье и материалов на один рубль продукции, коп.
| Номер | Х 1 | Х 2 | ХЗ | |
| предприятия | ||||
| 1 | 0,50 | 94,0 | 8,50 | |
| l-я группа | 2 | 0,67 | 75,4 | 8,79 |
| 3 | 0,68 | 85,2 | 9,10 | |
| 4 | 0,55 | 98,8 | 8,47 | |
| 5 | 1,52 | 81,5 | 4,95 | |
| 2-я группа | 6 | 1,20 | 93,8 | 6,95 |
| 7 | 1,46 | 86,5 | 4,70 |
Необходимо провести классификацию четырех новых предприятий, имеющих следующие значения исходных переменных:
l-е предприятие: 
= 1,07, 
=93,5, 
=5,30,
2-е предприятие: = 0,99, =84,0, =4,85,
3-е предприятие: = 0,70, =76,8, =3,50,
4-е предприятие: = 1,24, =88,0, =4,95.
Для удобства запишем значения исходных переменных для каждой группы предприятий в виде матриц 
и 
:
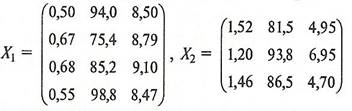(17)
Рассчитаем среднее значение каждой переменной в отдельных группах для определения положения центров этих групп:
I гр. 
=0,60, 
=88,4, 
=8,72
II гр. 
=1,39, 
=87,3, 
=5,53.
Дискриминантная функция f(x)в данном случае имеет вид:
f (х) = 
+
+
(18)
Коэффициенты 
, 
и 
вычисляются по формуле:
A=
(
-
), (19)
где и - векторы средних в первой и второй группах; А - вектор коэффициентов; 
- матрица, обратная совместной ковариационной матрице.
Для определения совместной ковариационной матрицы 
нужно рассчитать матрицы 
и 
. Каждый элемент этих матриц представляет собой разность между соответствующим значением исходной переменной 
и средним значением этой переменной в данной группе 
( k - номер группы):
Тогда совместная ковариационная матрица будет равна:
, (20)
где 
, 
- число объектов l-й и 2-й группы;
(21)
Обратная матрица будет равна:
.(22)
Отcюда находим вектор коэффициентов дискриминантной функции по формуле:
(23)
т.е. 
=-185,03, =1,84, =4,92.
Подставим полученные значения коэффициентов в формулу (18) и рассчитаем значения дискриминантной функции для каждого объекта:
(24)
Тогда константа дискриминации С будет равна:
С =
(94,4238-70,0138) = 12,205.
После получения константы дискриминации можно проверить правильность распределения объектов в уже существующих двух классах, а также провести классификацию новых объектов.
Рассмотрим, например, объекты с номерами 1, 2, З, 4. Для того чтобы отнести эти объекты к одному из двух множеств, рассчитаем для них значения дискриминантных функций (по трем переменным):
= -185,03 х 1,07 + 1,84 х 93,5 + 4,92 х 5,30 = 0,1339,
= -185,03 х 0,99 + 1,84 х 84,0 + 4,92 х 4,85 = -4,7577,