Реферат: Методы расчета электрических цепей постоянного тока
Под балансом мощностей электрической цепи понимается равенство мощностей, развиваемой всеми источниками энергии данной цепи, и мощности, потребляемой всеми приемниками той же цепи (закон сохранения энергии).
Если на участке цепи ab имеется источник энергии с ЭДС ![]() и по этому участку протекает ток
и по этому участку протекает ток ![]() , то мощность, развиваемая этим источником, определяется произведением
, то мощность, развиваемая этим источником, определяется произведением ![]() .
.
Каждый из множителей этого произведения может иметь положительный или отрицательный знак относительно направления ab. Произведение ![]() будет иметь положительный знак, если знаки расчетных величин
будет иметь положительный знак, если знаки расчетных величин ![]() и
и ![]() совпадают (мощность, развиваемая данным источником, отдается приемникам цепи). Произведение
совпадают (мощность, развиваемая данным источником, отдается приемникам цепи). Произведение ![]() будет иметь отрицательный знак если знаки
будет иметь отрицательный знак если знаки ![]() и
и ![]() противоположны (источник потребляет мощность, развиваемую другими источниками). Примером может служить аккумулятор, находящийся в режиме зарядки. В этом случае мощность данного источника (слагаемое
противоположны (источник потребляет мощность, развиваемую другими источниками). Примером может служить аккумулятор, находящийся в режиме зарядки. В этом случае мощность данного источника (слагаемое ![]() ) входит в алгебраическую сумму мощностей, развиваемых всеми источниками цепи, с отрицательным знаком. Аналогично определяется величина и знак мощности, развиваемой источником тока. Если на участке цепи mn имеется идеальный источник тока с током
) входит в алгебраическую сумму мощностей, развиваемых всеми источниками цепи, с отрицательным знаком. Аналогично определяется величина и знак мощности, развиваемой источником тока. Если на участке цепи mn имеется идеальный источник тока с током ![]() , то мощность развиваемая этим источником, определяется произведением
, то мощность развиваемая этим источником, определяется произведением ![]() . Как и в источнике ЭДС знак произведения
. Как и в источнике ЭДС знак произведения ![]() определяется знаками множителей.
определяется знаками множителей.
Теперь можно записать общий вид уравнения баланса мощностей
![]() .
.
Для цепи, представленной на рис2.2 уравнение баланса мощности имеет вид
![]() .
.
2. Метод контурных токов
Метод контурных токов сводится к составлению уравнений только по второму закону Кирхгофа. Число этих уравнений, равное ![]() , на
, на ![]() уравнений меньше числа уравнений, необходимых для расчета электрических цепей по методу законов Кирхгофа.
уравнений меньше числа уравнений, необходимых для расчета электрических цепей по методу законов Кирхгофа.
При этом предполагаем, что в каждом выбранном контуре протекает независимые друг от друга расчетные токи, называемые контурными. Ток каждой ветви определяется как алгебраическая сумма контурных токов, замыкающихся через эту ветвь, с учетом принятых направлений контурных токов и знаков их величин.
Число контурных токов равно числу «ячеек» (элементарных контуров) схемы электрической цепи. Если рассматриваемая схема содержит источник тока, то независимые контуры необходимо выбирать так, чтобы ветвь с источником тока входила только в один контур. Для этого контура расчетное уравнение не составляется, так как контурный ток равен току источника.
Каноническая форма записи уравнений контурных токов для n независимых контуров имеет вид
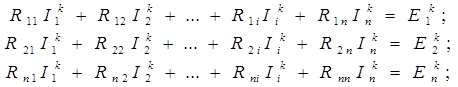 где
где
![]() - контурный ток n-го контура;
- контурный ток n-го контура;
![]() - алгебраическая сумма ЭДС, действующих в n-ом контуре, называемая контурная ЭДС;
- алгебраическая сумма ЭДС, действующих в n-ом контуре, называемая контурная ЭДС;
![]() - собственное сопротивление n-го контура, равная сумме всех сопротивлений, входящих в рассматриваемый контур;
- собственное сопротивление n-го контура, равная сумме всех сопротивлений, входящих в рассматриваемый контур;
![]() - сопротивление принадлежащие одновременно двум контурам (в данном случае контуром n и i ) и называемое общим или взаимным сопротивлением этих контуров. Первым ставится индекс контура, для которого составляется уравнение. Из определения взаимного сопротивления следует, что сопротивления, отличающиеся порядком индексов, равны, т.е.
- сопротивление принадлежащие одновременно двум контурам (в данном случае контуром n и i ) и называемое общим или взаимным сопротивлением этих контуров. Первым ставится индекс контура, для которого составляется уравнение. Из определения взаимного сопротивления следует, что сопротивления, отличающиеся порядком индексов, равны, т.е. ![]() .
.
Взаимным сопротивлением приписывается знак плюс, если протекающие по ним контурные токи ![]() и
и ![]() имеют одинаковые направления, и знак минус, если их направления противоположны.
имеют одинаковые направления, и знак минус, если их направления противоположны.
Таким образом, составление уравнений контурных токов может быть сведено к записи симметричной матрицы сопротивлений
![]()
и вектора контурных ЭДС
![]()
При введении вектора искомых контурных токов |![]() | уравнения (5) можно записать в матричной форме
| уравнения (5) можно записать в матричной форме
![]()
Решение системы линейных уравнений алгебраических уравнений (5) для тока n-го контура может быть найдено по правилу Крамера
 ,
,
где ![]() - главный определитель системы уравнений, соответствующий матрице контурных сопротивлений
- главный определитель системы уравнений, соответствующий матрице контурных сопротивлений

Определитель ![]() получаем из главного определителя
получаем из главного определителя ![]() путем замены n-го столбца сопротивлений на столбец (вектор) контурных ЭДС
путем замены n-го столбца сопротивлений на столбец (вектор) контурных ЭДС ![]() .
.