Фрактальный алгоритм позволяет сжимать изображения в сотни и даже тысячи раз.

Основная сложность фрактального сжатия заключается в том, что для нахождения соответствующих доменных блоков, требуется полный перебор.

Поскольку при этом переборе каждый раз должны сравниваться два массива, данная операция получается достаточно длительной, требующей значительных вычислительных ресурсов.

На сегодняшний день фрактальные методы наилучшим образом приспособлены для приложений архивирования, таких как цифровые энциклопедии, в которых кодирование необходимо лишь однажды, а декодирование происходит множество раз.

Фрактальные методы можно рассматривать, как альтернативу технологиям, основанным на преобразовании Фурье, например, таким как JPEG. Новые технологии, такие как фрактальные должны рассматриваться не только как конкуренты, но и как союзники в установлении новых стандартов.

Алгоритм SPIHT ( Пространственно Упорядоченные Иерархические Деревья) представляет собой метод сжатия изображений с потерями и обладает высокой чувствительностью. Его легко реализовывать, он работает быстро и дает прекрасные результаты при сжатии любых типов изображений.

Метод SPIHT был разработан для оптимальной прогрессирующей передачи изображений, а также для их сжатия. Самая важная особенностью этого алгоритма заключается в том, что на любом этапе декодирования качество отображаемой в этот момент картинки является наилучшим для введенного объема информации о данном образе.

Другая отличительная черта алгоритма SPIHT состоит в использовании им вложенного кодирования. Это свойство можно определить следующим образом: если кодер, использующий вложенное кодирование, производит два файла, большой объема М бит и маленький объема nбит, то меньший файл совпадает с первыми Mбитами большего файла.

Следующий пример удачно иллюстрирует это определение. Предположим, что три пользователя ожидают некоторое отправленное им сжатое изображение. При этом им требуется различное качество этого изображения. Первому из них требуется качество, обеспечиваемое 10 KB образа, а второму и третьему пользователю необходимо качество, соответственно, в объеме 20 KB и 50 КВ. Большинству методов сжатия изображения с частичной потерей данных потребуется сжимать исходный образ три раза с разным качеством, для того, чтобы сгенерировать три различных файла, требуемых объемов. А метод SPIHT произведет для этих целей всего один файл, и пользователям будут посланы три начальных фрагмента этого файла, длины которых соответственно равны 10 KB,20 KB и 50 КВ.

На одном из его этапов применяется вейвлетное преобразование. Кроме того, основная структура данных этого алгоритма, пространственно ориентированное дерево, использует тот факт, что различные поддиапазоны отражают разные геометрические особенности образа. Преобразования Хаара можно применять к изображению несколько раз подряд. При этом образуются различные области (поддиапазоны), состоящие из средних и деталей данного образа. Преобразование Хаара является очень простым и наглядным, но для лучшего сжатия стоит использовать другие вейвлетные фильтры, которые лучше концентрируют энергию изображения.

Различные вейвлетные фильтры будут давать разные коэффициенты сжатия для разных типов изображений. Однако исследователям пока не до конца ясно, как построить наилучший фильтр для каждого типа образов. Независимо от конкретно используемого фильтра, образ разлагается на поддиапазоны так, что нижние поддиапазоны соответствуют высоким частотам изображения, а верхние поддиапазоны отвечают низким частотам образа, в которых концентрируется основная часть энергии изображения. Поэтому можно ожидать, что коэффициенты деталей изображения уменьшаются при перемещении от высокого уровня к более низкому. Кроме того, имеется определенное пространственное подобие между поддиапазонами. Части образа, такие как пики, занимают одну и ту же пространственную позицию во всех поддиапазонах.

Рисунок 2 - поддиапазоны и уровни вейвлетного разложения.

Начнем с общего описания метода SPIHT. Обозначим пикселы исходного изображения р через pij. Любое множество фильтров Т может быть использовано для преобразования пикселов в вейвлетные коэффициенты (или коэффициенты преобразования) Cij. Эти коэффициенты образуют преобразованный образ с. Само преобразование обозначается с = Т (р). При прогрессирующем методе передачи декодер начинает с того, что присваивает значение ноль реконструированному образу с. Затем он принимает (кодированные) преобразованные коэффициенты, декодирует их и использует для получения улучшенного образа с, который, в свою очередь, производит улучшенное изображение р = Т-1 (с). Основная цель прогрессирующего метода состоит в скорейшей передаче самой важной части информации об изображении. Эта информация дает самое большое сокращение расхождения исходного и реконструированного образов. Для количественного измерения этого расхождения метод SPIHT использует среднеквадратическую ошибку MSE (mean squared error).

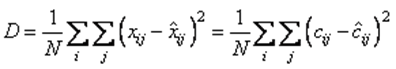
Самые большие (по абсолютной величине) коэффициенты Cij несут в себе информацию, которая больше всего сокращает расхождение MSE, поэтому прогрессирующее кодирование должно посылать эти коэффициенты в первую очередь. В этом заключается первый важный принцип SPIHT. Другой принцип основан на наблюдении, что наиболее значимые биты двоичных представлений целых чисел стремятся быть единицами, когда эти числа приближаются к максимальным значениям. (Например, в 16-битном компьютере число +5 имеет представление 0|000.0101, а большое число +65382 запишется в виде 0|111111101100110. Это наводит на мысль, что старшие биты содержат наиболее значимую часть информации, и их также следует посылать (или записывать в сжатый массив данных) в первую очередь.

Главным недостатком этого алгоритма является большой объем информации координат передаваемых значимых коэффициентов . Для того чтобы оптимизировать данный процесс в алгоритме SPIHT поступают следующим образом. Разбивают все множество коэффициентов на подмножества , например, так как показано на рисунке 3.

Рисунок 3 - пример расположения множеств T_k

Затем, просматривают каждое множество и проверяют, имеются ли в них значимые коэффициенты , т.е. коэффициенты, удовлетворяющие условию . Если найден в множестве хотя бы один такой коэффициент, то такое множество также считается существенным. Предположим, что в нашем примере значимым множеством является только . Тогда оно разбивается на подмножества , для которых выполняется такая же проверка коэффициентов . И так далее пока не дойдем до множеств, состоящих из одного коэффициента. В результате декодеру передается битовая информация, указывающая, является ли конкретное множество значимым или нет. Благодаря иерархической структуре множеств , общий объем информации о расположении значимых коэффициентов становится меньше, чем простая передача их координат.

Основные шаги кодера SPIHT

Шаг 1 : Для заданного сжимаемого изображения вычислить его вейвлетное преобразование, используя подходящие вейвлетные фильтры, разложить его на коэффициенты преобразования qj и представить их в виде целых чисел фиксированной разрядности. Предположим, что коэффициенты представлены в виде целых чисел со знаком, разрядность которых равна 16, причем самый левый бит является знаковым, а в остальных двоичных 15 разрядах записан модуль этого числа. (Отметим, что такое представление отличается от комплементарного представления чисел со знаком, которое традиционно применяется в компьютерах.) Значения этих чисел меняются в диапазоне от - (2¹⁵ - 1) до (2¹⁵ - 1). Присвоим переменной nзначение n= [log2 (2¹⁵ - 1) J = 14.

Шаг 2: Сортировка. Передать число I коэффициентов которые удовлетворяют неравенству 2n< \c_{, ij} \ < 2n+1. Затем передать I пар координат и I знаков этих коэффициентов.

Шаг 3: Поправка. Передать (n - 1) - ые самые старшие биты всех коэффициентов, удовлетворяющих неравенству \c{j\ > 2n. Эти коэффициенты были выбраны на шаге сортировки предыдущей итерации цикла (не этой итерации!).

Шаг 4: Итерация. Уменьшить nна 1. Если необходимо сделать еще одну итерацию, пойти на Шаг 2. Обычно последняя итерация совершается при n= 0, но кодер может остановиться раньше. В этом случае наименее важная часть информации (некоторые менее значимые биты всех вейвлетных коэффициентов) не будет передаваться. В этом заключается естественное отбрасывание части информации в методе SPIHT. Это эквивалентно скалярному квантованию, но результат получается лучше, поскольку коэффициенты передаются в упорядоченной последовательности. В альтернативе кодер передает весь образ (то есть, все биты всех вейвлетных коэффициентов), а декодер может остановить процесс декодирования в любой момент, когда восстанавливаемое изображение достигло требуемого качества. Это качество или предопределяется пользователем, или устанавливается декодером автоматически по затраченному времени.

Рассмотрим подробно, что собой представляет кодирование в алгоритме SPIHT

Прежде всего отметим, что кодер и декодер должны использовать единый тест при проверке множеств на существенность. Алгоритм кодирования использует три списка, которые называются: список существенных пикселов (LSP, list of significant pixels), список несущественных пикселов (LIP, list of insignificant pixels) и список несущественных множеств (LIS, list of insignificant sets).

В эти списки заносятся координаты (i,j) так, что в списках LIP и LSP они представляют индивидуальные коэффициенты, а в списке LIS они представляют или множество T> (i,j), или множество C (i,j).

Список LIP содержит координаты коэффициентов, которые были несущественными на предыдущей стадии сортировки. В текущей стадии они проверяются, и если множество является существенным, то они перемещаются в список LSP. Аналогично множества из LIS тестируются в последовательном порядке, и если обнаруживается, что множество стало существенным, то оно удаляется из LIS и разделяется.

Новые подмножества, состоящие более чем из одного элемента, помещаются обратно в список LIS, где они позже будут подвергнуты тестированию, а одноэлементные подмножества проверяются и добавляются в список LSP или LIP в зависимости от результатов теста. Стадия поправки передает n-ный самый старший бит записей из списка LSP.