Реферат: Микроструктура керамики, полученной прессованием в поле акустических волн

Качество керамики напрямую связано с получением пресс-заготовок высокой плотности. Раннее [1-3] показано, что при одноосном прессовании с применением ультразвуковых колебаний (УЗК) пористость керамики ВаТiO₃ уменьшается, что обусловливает улучшение физико-механических свойств готовых изделий.

Объектом исследования в данной работе выбрана керамика ЦТБС-3М, гистограмма распределения по размерам зерен предварительно синтезированного порошка после сухого помола которой приведена на рис.1.

Рис.1– Гистограмма распределения по среднему размеру частиц порошка ЦТБС-3М.

Пресс-заготовки получали в одноосной пресс-форме диаметром 7,2 мм, высота прессовки составляла 3,5 мм. Ультразвуковые колебания частотой 22 кГц, мощностью 0,4 кВт и амплитудой 10-12 мкм подводили к прессовке в направлении прессования через пуансон. Давление прессования изменяли в диапазоне (1÷4,5)∙10⁸ Па. Время выдержки при максимальном давлении составляло до 30 с. В качестве связки использовали 7% раствор поливинилового спирта, который вводили в прессуемый порошок в количестве до 3,5 весовых процента.

Пресс-заготовки получали по заводской технологии протяжкой (РУП «Монолит), прессованием без наложения УЗК и с воздействием на порошок УЗК (рис. 2). Кроме того, порошок керамики перед прессованием в течении 60 с. подвергали ультразвуковой обработке в жидкой среде(рис. 3) и затем прессовали без связки (рис.4).

1 2 3

Рис. 2 – Микроструктура керамики ЦТБС-3М: 1- протяжка; 2-обычное одноосное прессование; 3- прессование в ультразвуковом поле. Количество связки 3,5 весовых процента.

1 2

Рис.3 - Микроструктура порошка ЦТБС-3М: 1 – исходный материал; 2 - после предварительной ультразвуковой обработки

1 2

Рис. 4– Микроструктура керамики ЦТБС-3М полученной: прессованием в ультразвуковом поле для исходного порошка – 1, порошка предварительно обработанного в ультразвуковом поле – 2.

Исследованиями установлено, что воздействие ультразвуковых колебаний на исходный порошок через жидкую среду приводит к его некоторому измельчению за счет разрушения агломератов. Сравнение микроструктуры керамики ЦТБС-3М, полученной различными методами, позволяет сделать вывод, что наименьшая пористость наблюдается у образцов, синтезированных из пресс-заготовок, полученных из порошка, предварительно обработанного в ультразвуковом поле и спрессованного с применением УЗК без связки. При этом удается обеспечить более равномерное распределение зерен по размерам.

Основной целью настоящей работы является моделирование определяющих соотношений в необратимом процессе поляризации сегнетоэлектрических керамик, в которых наравне с большими электрическими полями имеются связанные механические напряжения, влияющие на процесс поляризации. При моделировании необратимых процессов вводят дополнительные параметры, описывающие ту или иную необратимость, например, тензор пластических деформации в пластических средах, вектор остаточной поляризации в сегнетоэлектриках и т.д. Однако для замыкания задачи необходимо введение дополнительных определяющих соотношений. Как правило, такие соотношения строятся для одномерных задач с привлечением каких-либо реологических моделей, а затем переносятся на трехмерный случай. Например, в теории пластичности реологическими элементами являются упругий элемент Гука (пружина) и пластический элемент Сен-Венана (элемент сухого трения). Детальный механизм пластичности конкретного материала на микроскопическом уровне не рассматривается, но для выявления специфики протекающего процесса в том или ином теле создают различные комбинации последовательного и параллельного соединения этих элементов, получая соответствующие модели, наиболее общими из которых являются модели Прандтля-Ишлинского и Прагера. Переход от одномерного к трехмерному случаю можно осуществить с помощью элементов выпуклого анализа и получить ассоциированный закон течения, который и выступает в качестве искомых определяющих соотношений [1]-[2]. В теории пластичности такой подход является приемлемым и во многих случаях дает хорошее согласие с экспериментом. Однако в тории поляризации ситуация резко меняется, для получения согласованных с экспериментом законов необходимо проводить более тонкий учет перестройки внутренней структуры материала, особенно в поликристаллических сегнетоэлектриках.

В настоящей работе представлена модель поляризации сегнетоэлектрического поликристаллического диэлектрика, позволяющая находить приращение остаточного вектора поляризации и тензора деформации в зависимости от приращения электрического поля. Модель строится с помощью элементов двухуровневой сплошной среды: вначале с помощью электрического поля Вейсса и статистики Больцмана получена предельная зависимость поляризации от электрического поля; затем с учетом кинематических соотношений и балансного энергетического соотношения получено обыкновенное дифференциальное уравнение, из которого выводятся искомые зависимости. В одномерном случае предложенная модель совпадает с моделью Джила-Атертона [3].

Численные результаты, полученные по разработанной модели, представлены на рис. 2, где приведены графики приращения остаточной поляризации для положительного и отрицательного приращения электрического поля, когда оно, изменяясь по модулю, сохраняет свое направление. Слева указаны начальные значения точек, от которых отсчитывалось приращение продольной составляющей поля. На рис. 3 представлены гистерезисные кривые, полученные с помощью этой же модели, когда электрическое поле изменялось циклически. Сплошной линией показана петля полной поляризации, а пунктирной - остаточной. Модель имеет 5 параметров, с помощью которых можно описать любую петлю.

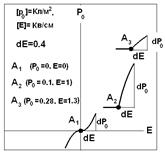
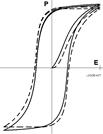
Рис. 5. Рис. 6.

Результаты работы используются в моделях для расчета полей остаточной поляризации и остаточной деформации в сильных электрических полях.

Необходимость получения достоверной информации о микроскопическом устройстве дефекта делает актуальной задачу поиска соответствующих методов обработки макроскопических характеристик, в частности температурной зависимости концентрации основных носителей (ТЗКН) в полупроводнике при различных степенях компенсации в соответствующих температурных интервалах. Один из таких методов был предложен в работе [1], развитие его получило в работах [2-7]. Основная идея метода состоит в применении дифференциальной обработки ТЗКН в условиях различного темпа изменения концентрации свободных носителей n и энергии Ферми E_F с температурой T. Было замечено что, если электронные уровни дефектов расположены достаточно далеко друг от друга, то функция размерности концентрации

Y(E_F )≡k_B T(dn/dE_F )

(k_B – постоянная Больцмана) от энергии Ферми имеет вид спектральных полос. По положению максимумов этой функции на оси E_F и их величине определяют энергетический спектр в запрещенной зоне и концентрацию дефектов, соответственно. Сравнивая полуширину полосы с температурой, при которой наблюдается максимум, как было показано в работах [3-4], можно определить, обладает ли данный дефект U^– -свойствами.

На практике, используя экспериментальные данные по ТЗКН – n(T), строят функцию Y(E_F ) по формуле:

Y(E_F )=k_B [(T_i+1 +T_i )/2][n(T_i+1 ) – n(T_i )]/[E_F (T_i+1 ) – E_F (T_i )],

где n(T_i ) – экспериментальное значение концентрации свободных носителей при температуре T_i ; E_F (T_i )≡k_B T_i ln(N_C (T_i )/n(T_i )) – энергия Ферми, рассчитанная на основе экспериментальных данных по n(T_i ); N_C (T_i ) – плотность состояний в зоне проводимости при температуре T_i . Выбор шага {T_{i +1} , T_i } определяется экспериментальной точностью двух различных значений n.

Данный метод использовался в частности для определения параметров таких дефектов как вакансии в кремнии [3-4], кислородные термодоноры в Si [7-8] и Ge [9], а также водородсодержащие доноры в кремнии [10].

Цель нашей работы состоит в выявлении (обнаружении) условий, при которых возникают трудности интерпретации данных, полученных методом дифференциального анализа ТЗКН, которые могут приводить к ошибочным заключениям об образовании новых дефектов при внешних воздействиях.

Как показали результаты наших исследований, применение метода дифференциального анализа ТЗКН для определения параметров амфотерных центров может привести к особенностям при определении энергии акцепторного состояния в запрещенной зоне полупроводника для амфотерных дефектов и их концентрации в различных условиях компенсации.

Результаты численного расчета Y(E_F ) для амфотерного центра с прямым порядком следования электронных уровней (т.е. E_a <E_d , E_a и E_d – энергия акцепторного состояния и энергия донорного состояния амфотерных центров в запрещенной зоне полупроводника, соответственно) показали, что в случае некомпенсированного полупроводника будет наблюдаться максимум характеристики Y(E_F ), связанный только с донорным уровнем амфотерного центра. При незначительном уровне компенсации (т.е. концентрация мелких доноров N_d на много меньше концентрации амфотерных центров N) можно наблюдать дополнительный пик, который связан с акцепторным состоянием дефекта, но при этом положение максимума Y(E_F )-характеристики не соответствует энергии ионизации данного акцепторного уровня и смещено в область больших энергий. Такое поведение характеристики Y(E_F ) связано с тем, что уровень Ферми в данных условиях не пересекает электронный уровень акцепторного состояния амфотерного центра с изменением температуры. Следует отметить, что концентрация акцепторных состояний, определенная методом дифференциального анализа ТЗКН при незначительном уровне компенсации соответствует концентрации компенсирующих мелких донорных центров и существенно отличается от концентрации донорных состояний амфотерных центров, определенной тем же способом. Так что, представляется затруднительным связывать полученные результаты с одним и тем же дефектом.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--