Реферат: Минимизация функции многих переменных Приближённые численные методы Метод Монте-Карло

откуда получаем критические точки: А(0;0); В(3;2). Исследуем эти точки. Для этого нам нужно выяснить, в каждой из этих точек, к какому виду принадлежит квадратичная форма:

(10)

(11)

(12)

(13)

В точке A(0;0) имеем:

,

так что , и условия критерия

Сильвестра не дают ответа на вопрос о наличии экстремума в этой точке.

Для решения этого вопроса надо привлечь старшие производные и формы более высокого порядка, для которых соответствующей общей теории пока нет, поэтому нужно обращаться к численным исследованиям.

В точке B(3;2) имеем:

,

получаем матрицу квадратичной формы:

.

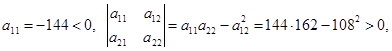
т.е. по критерию Сильвестра B(3;2) является точкой максимума:

2. Метод градиентного спуска.

Как мы видели из последнего численного примера, строгий аналитический метод не всегда приводит к цели (случай, когда в критической точке). В подобных, и в более сложных случаях применяют различные приближённые аналитические методы, которые в математическом смысле иногда менее строго обоснованы, но, тем не менее порой приводят к желаемому результату. К таким методам относятся и градиентные методы наискорейшего спуска.

Пусть, нам нужно найти . Рассмотрим некоторую точку и вычислим в этой точке градиент функции :

(14)

где - ортонормированный базис в пространстве . Если , то полагаем:

(15)

где , а выбирается из условия сходимости итерационного процесса:

(16)

где , а выбираются из условия сходимости. Формулу (16) можно расписать в виде:

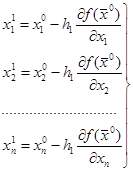первое приближение; (17)

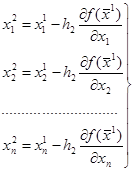второе приближение; (18)

………………………..

m-тое приближение; (19)