Реферат: Многофункциональность упражнения и многофакторность умения
А.В. Ястребов, Ярославский государственный педагогический университет
В работе сформулированы два положения, связанные с процессом формирования математических умений. Проведено их обсуждение с точки зрения некоторых современных концепций преподавания математики.
Основные утверждения
Первое утверждение, которое мы назовём многофункциональностью упражнения, формулируется так: упражнение формирует, как правило, не одно умение, а целую группу умений.
Проиллюстрируем это на материале курса алгебры и теории чисел. Для этого рассмотрим следующую задачу.
Задача. Подкольцо Z кольца R порождает бинарное отношение T на R следующим образом:
![]()
![]()
![]()
![]() .
.
Является ли T отношением эквивалентности? Если да, то найдите фактор-множество R/T.
Прежде всего отметим, что появление такой задачи при изучении отношений эквивалентности вполне естественно. Действительно, при построении теории чисел в рамках базового курса алгебры и теории чисел мы вместо включения Z R используем включение Gm Z, где Gm - множество чисел, кратных m 0, 1, а вместо бинарного отношения T - отношение сравнения ≡ по модулю m ; сами же отношения T и ≡ определяются единообразно.
Доказательство того факта, что T - отношение эквивалентности, основано на свойствах операций над вещественными числами. Например, транзитивность доказывается следующим образом:
![]()
Переходя к описанию фактор-множества нетрудно заметить, что любые различные числа полусегмента [0, 1) попарно неэквивалентны, и что любое вещественное число эвкивалентно одному из чисел данного полусегмента. Таким образом, фактор-множество построено, однако результат построения недостаточно хорош, поскольку с тем же основанием можно назвать фактор-множеством многие другие объекты, например, полусегмент [a, a+1) при произвольном a, полуинтервал (а, а+1], объединение сегмента и интервала ![]() и т.д. Для канонического описания фактор-множества нужно вспомнить, что полусегмент [0, 1) находится во взаимно-однозначном соответствии с полусегментом [0, 2 ), который, в свою очередь, находится во взаимно-однозначном соответствии с окружностью S, заданной стандартными параметрическими уравнениями. Образуя композицию этих соответствий, мы можем получить каноническое отображение
и т.д. Для канонического описания фактор-множества нужно вспомнить, что полусегмент [0, 1) находится во взаимно-однозначном соответствии с полусегментом [0, 2 ), который, в свою очередь, находится во взаимно-однозначном соответствии с окружностью S, заданной стандартными параметрическими уравнениями. Образуя композицию этих соответствий, мы можем получить каноническое отображение ![]() , определяемое параметрическими уравнениями
, определяемое параметрическими уравнениями
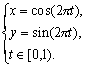
Итак, фактор-множество является окружностью: R/T=S.
Приведённая схема решения показывает, что задача по своему происхождению является алгебраической, результат формулируется на геометрическом языке, а значительная часть доказательства осуществляется с помощью техники, характерной для математического анализа. Действительно, данная задача формирует группу разнохарактерных умений.
Отступим от основной линии изложения и наметим развитие данной задачи в двух направлениях, геометрическом и алгебраическом.
Отношение T на R порождает бинарное отношение T1![]() на множестве R2, которое определяется следующим образом:
на множестве R2, которое определяется следующим образом:
![]()
Другими словами, две точки из R2 находятся в бинарном отношении T1, если их первые координаты эквивалентны в смысле отношенияT.
Нетрудно доказать, что T1 - отношение эквивалентности. Из его определения вытекает, что для факторизации R2 = R R по T1 нужно профакторизировать по T первый множитель декартова произведения, откуда следует, что R2/T1=(R/T) R=S R. Очевидно, что декартово произведение окружности S на прямую R является цилиндром.
Аналогично, отношение T на R порождает бинарное отношение T2 на множестве R2, которое определяется следующим образом:
![]()
Другими словами, две точки из R2 находятся в бинарном отношении T2, если их соответственные координаты эквивалентны в смысле отношения T.
Нетрудно доказать, что T2 - отношение эквивалентности. Из его определения вытекает, что для факторизации R2 = R R по T2 нужно профакторизировать по T каждый множитель декартова произведения, откуда следует, что R2/T2 = (R/T) (R/T)=S S. Декартово произведение двух окружностей - это тор. Таким образом, исходная алгебраическая задача получила хорошее геометрическое продолжение.
Эту же задачу можно рассматривать с точки зрения теории групп, поскольку (R, +) - это группа. Каждое вещественное число a порождает класс эквивалентности ā R/T. Если определить операцию сложения на R/T с помощью формулы ![]() то можно доказать, что это определение корректно и что пара (R/T, +)образует группу.
то можно доказать, что это определение корректно и что пара (R/T, +)образует группу.
Вспомним теперь об отождествлении фактормножества с окружностью: классы эквивалентности ā и ![]() из фактормножества соответственно отождествляются с точками
из фактормножества соответственно отождествляются с точками ![]()
![]() и
и ![]() на окружности. В силу этого операция сложения классов индуцирует операцию сложения точек:
на окружности. В силу этого операция сложения классов индуцирует операцию сложения точек: ![]() . Естественно поставить вопрос о том, как найти положение точки C на окружности, зная положения точек A и B. Совершенно аналогично можно построить операции над точками цилиндра и тора и поставить задачу о выяснении геометрического смысла этих операций. Таким образом, как исходная задача, так и её продолжение формирует целую группу умений из различных разделов математики.
. Естественно поставить вопрос о том, как найти положение точки C на окружности, зная положения точек A и B. Совершенно аналогично можно построить операции над точками цилиндра и тора и поставить задачу о выяснении геометрического смысла этих операций. Таким образом, как исходная задача, так и её продолжение формирует целую группу умений из различных разделов математики.
Второе из основных утверждений, которое мы назовём многофакторностью умения, формулируется так: умение формируется, как правило, под воздействием многих разнохарактерных упражнений.
Дело в том, что умение нельзя считать сформированным в момент сообщения студенту его формально-логической базы, т.е. формулы, теоремы, алгоритма и т.д. Для его полного формирования необходима как стадия пропедевтики, так и стадия применения. Последняя, в свою очередь, состоит из двух частей: непосредственного применения и вхождения умения в качестве составной части в более сложный комплекс умственных действий. Например, вряд ли можно считать, что учащийся овладел тригонометрическими формулами в тот момент, когда они были впервые выведены преподавателем или даже получены самостоятельно. Их полное освоение происходит в процессе решения тригонометрических уравнений и неравенств, доказательства тригонометрических тождеств, исследования тригонометрических функций, вычисления тригонометрических интегралов, действий с комплексными числами, записанными в тригонометрической форме, и.т.д. Умение приводить матрицу к ступенчатому виду оказывается полностью сформированным в результате решения систем линейных уравнений, исследования таких систем с параметрами, применения метода неопределённых коэффициентов в алгебое и математическом анализе, выполнения более чем полутора десятков алгоритмов линейной алгебры. Умение дифференцировать формируется не только при выполнении упражнений на технику дифференцирования, но также при исследовании функций и построении их графиков, при дифференцировании интегралов с переменным верхним пределом, при исследовании функций многих переменных, при изучении функций комплексного переменного.
Перечисленные и многие другие примеры выявляют одно объективное обстоятельство: многие математические умения и навыки, которые начали формироваться ещё в школе, доводятся до совершенства в вузе в процессе решения упражнений и задач самых разнообразных типов.
Основные утверждения в свете некоторых методических концепций
Рассмотрим сформулированные выше основные утверждения с точки зрения трёх методических концепций: авторской концепции обучения математике как модели научных исследований [5], теоретических основ подготовки преподавателей профильных школ О.А. Иванова [1] и технологии наглядно-модельного обучения Е.И. Смирнова [4].
--> ЧИТАТЬ ПОЛНОСТЬЮ <--